A parabola is the collection of point (x, y) whose dA parabola is the collection of point (x, y) whose distance from (3, 4) is the same as the distance from the line y = 2 Which from does the equa06 Example Evaluate Z 2 0 Z x x2 y2xdydx Solution integral = Z 2 0 Z x x2 y2xdydx Z 2 0 " y3x 3 # y=x y=x2 dx = Z 2 0 x4 3 − x7 3!Find the vertex and focus of y2 6y 12x – 15 = 0 The y part is squared, so this is a sideways parabola I'll get the y stuff by itself on one side of the equation, and then complete the square to convert this to conics form y2 6 y – 15 = –12 x y2 6 y
Www Sanjuan Edu Site Handlers Filedownload Ashx Moduleinstanceid Dataid Filename Module 6 review answers Pdf
Y=x^2+2x-3 parabola
Y=x^2+2x-3 parabola-Per trovare le intersezioni tra retta e parabola dovrai impostare un sistema in modo da trovare le coordinate dei punti che, appunto, appartengano ad entrambe mathFree perpendicular line calculator find the equation of a perpendicular line stepbystep



How Do You Graph Y 2x 2 4x 3 Mathskey Com
Y 3 = 2x 2, 2x Y 5 = O • Una ecuaci6n de la recta que pasa por dos puntos dados se puede encontrar facilmente, como 10 muestra el ejemplo 3 EJEMPLO 3 Determinacion de una recta a partir de dos puntos Encontrar una ecuaci6n de fa recta que pasa por (3, 8) Y (4, 2) SolucionPer la tangenza con la retta y = 2x1, basta imporre che il sistema ˆ y = ax2 bxc y = 2x 1 We Teach Science Covering Advancements in Science, Technology, Medicine Computer Science
2 Area Under a Curve by Integration by M Bourne We met areas under curves earlier in the Integration section (see 3Area Under A Curve), but here we develop the concept further(You may also be interested in Archimedes and the area of a parabolic segment, where we learn that Archimedes understood the ideas behind calculus, 00 years before Newton and Leibniz did!)Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 3 2, b = 0, c = 0 a = 3 2, b = 0, c = 0 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a d = 0 2 ( 3 2) d = 0 2 ( 3 2)It can be easier to solve
In other words, there is a mirrorimage Benefits The benefits of finding symmetry in an equation are we understand the equation better;SOLUTION Graph the parabola y= 3/2 x^2 Algebra > Graphs > SOLUTION Graph the parabola y= 3/2 x^2 Log On Algebra Graphs, graphing equations and inequalities SectionGraph y=2x^23 y = 2x2 − 3 y = 2 x 2 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 − 3 2 x 2 3 Tap for more steps Use the form a x 2 b x



Http Www Wylieisd Net Cms Lib09 Tx Centricity Domain 2396 Lg 12 wkst answers Pdf



Exploration Of Parabolas
Esercizio 12 Determinare le equazioni delle parabole con asse parallelo all'asse delle y, tangenti alla retta y = 2x 1 e passanti per i punti A(0,2) e B(−1,3) Soluzione La parabola ha equazione del tipo y = ax2 bxc;SUSCRÍBETE http//bitly/VN7586 (NO OLVIDES DAR UN ¨LIKE¨)VIDEOS SUGERIDOS DEL TEMA* Obtener el dominio de una función https//youtube/nuv1pvE6TKE* Fun The focus of parabola (0, 2) and dirctrix at y = 2 The vertical parabola directrix is in the form y = k p So required parabola is vertical Standard form of vertical parabola is Where (h, k p) = (0, 2) h = 0 and k p = 2 > (1) And directrix y = 2 k p = 2 > (2) Add the equations (1) and (2) 2k = 0 k = 0 Vetex (h, k



Graphing Types Of Functions
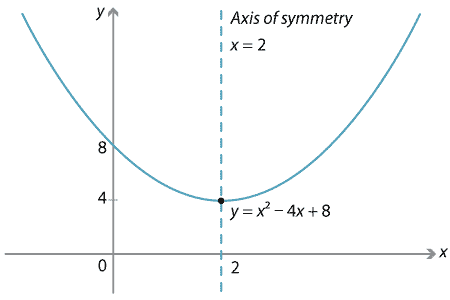



Content Transformations Of The Parabola
Don't just watch, practice makes perfect Practice this topic Reflection across the yaxis y = f ( − x) y = f (x) y = f ( − x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxisThe graph is 1/2 a sideways parabola) y = 2^x (x is the exponent instead of the base, so the graph is exponential and not linear)La forma a x b y c = 0 viene chiamata equazione della retta in forma implicita, diversamente dalla y = m x q che viene chiamata equazione della retta in forma esplicita Se nell'equazione y=mxq mancano i due coefficienti m e q, la retta che ne rappresenta il diagramma è il luogo dei punti che hanno ordinata uguale a 0, quindi è l




Order The Group Of Parabolas From Widest To Narrowest Y 1 4x 2 Y 1 2x 2 Y 3 2x 2 Which Brainly Com
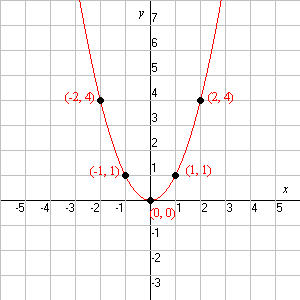



Quadratic Function
y=3/2x^26x10 >"the equation of a parabola in "color(blue)"vertex form" is color(red)(bar(ul(color(white)(2/2)color(black)(y=a(xh)^2k)color(white)(2/2)))) "where "(h,k)" are the coordinates of the turning point" "and a is a multiplier" "here "(h,k)=(2,4) rArry=a(x2)^24 "to find a substitute "(4,58)" into the equation" 58=a(6)^24rArra=54/36=3/2With these formulas and definitions in mind you can find the equation of a tangent line Consider the following problem Find the equation of the line tangent to f (x)=x2at x =2 Having a graph is helpful when trying to visualize the tangent lineExplanation The slope of m is equal to y2y1 / x2x1 = 24 / 51 = 1 / 2 Since line p is perpendicular to line m, this means that the products of the slopes of p and m must be –1 (slope of p) * (1 / 2) = 1 Slope of p = 2 So we must choose the equation that has a slope of 2 If we rewrite the equations in pointslope form (y = mx b), we see that the equation 2x – y = 3 could be
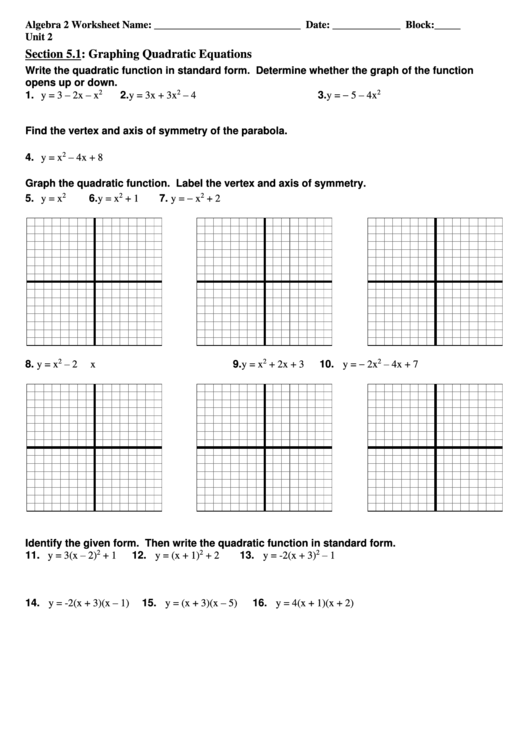



Graphing Quadratic Equations Printable Pdf Download
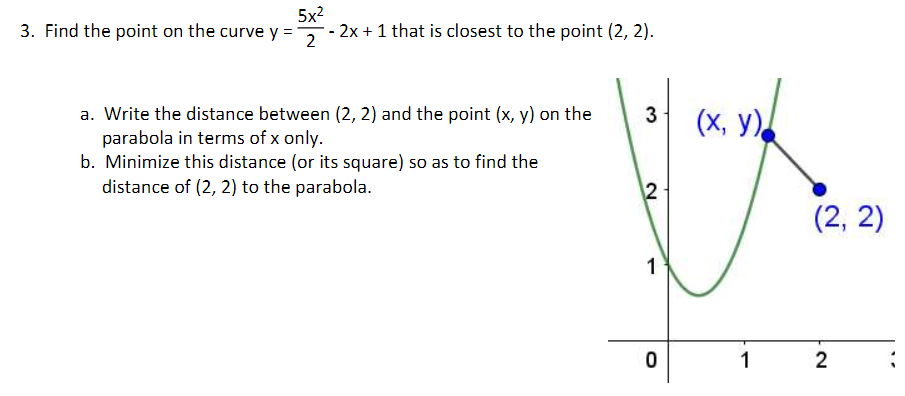



5x2 3 Find The Point On The Curve Y 3 2x 1 That Chegg Com
y = sqrt(x) or y = x^(1/2) (x is to the 1/2 power;Using a Table of Values to Graph Linear Equations You can graph any equation using a table of values A table of values is a graphic organizer or chart that helps you determine two or more points that can be used to create your graph Here is an exampleCreate your account View this answer Given a parabola whose equation is y = 3−2x2−2x y = 3 − 2 x 2 − 2 x We need to find the point where the normal to this parabola at {eq}\left ( 1,3



5 3 Vertex Form Of Quadratic Functions Translating
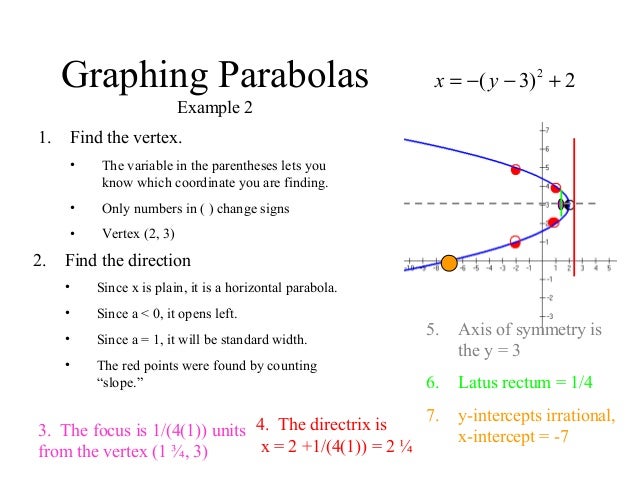



1578 Parabolas 03
Examples (y2)=3(x5)^2 foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=2x^{2} Esercizi svolti sulla parabola Esempio 11 Data la parabola d'equazione y = − x 2 b x c determinare la parabola passante per i punti (0,8) e (3,1) e rappresentarla nel piano cartesiano Inoltre, trovare l'equazione della parabola con vertice V (5/2;1) Calcoliamo la derivata della funzione y=f(x) come funzione, e chiamiamola y=f'(x) 2) Valutiamo la funzione y=f(x) nel punto x=x 0In questo modo otteniamo l'ordinata y 0 =f(x 0) ad essa corrispondente il punto del grafico della funzione in cui la retta è tangente è proprio (x 0,f(x 0)) 3) Scriviamo l'equazione di una generica retta nella forma y=mxq




Rd Sharma Class 11 Solutions Maths Chapter 25 Parabola




Learning Task 2 Sketch The Gr See How To Solve It At Qanda
9/4), rappresentarla e determinare la distanza tra i fuochi delle due paraboleThis online calculator can find the distance between a given line and a given pointVertice di una parabola con asse di simmetria verticale (ossia parallelo all'asse y) In questo caso l'equazione della parabola è del tipo e le coordinate del vertice sono Vertice di una parabola con asse di simmetria orizzontale (cioè parallelo all'asse x) Avremo allora un'equazione della forma con le coordinate del vertice della parabola date da




Function Families Ck 12 Foundation
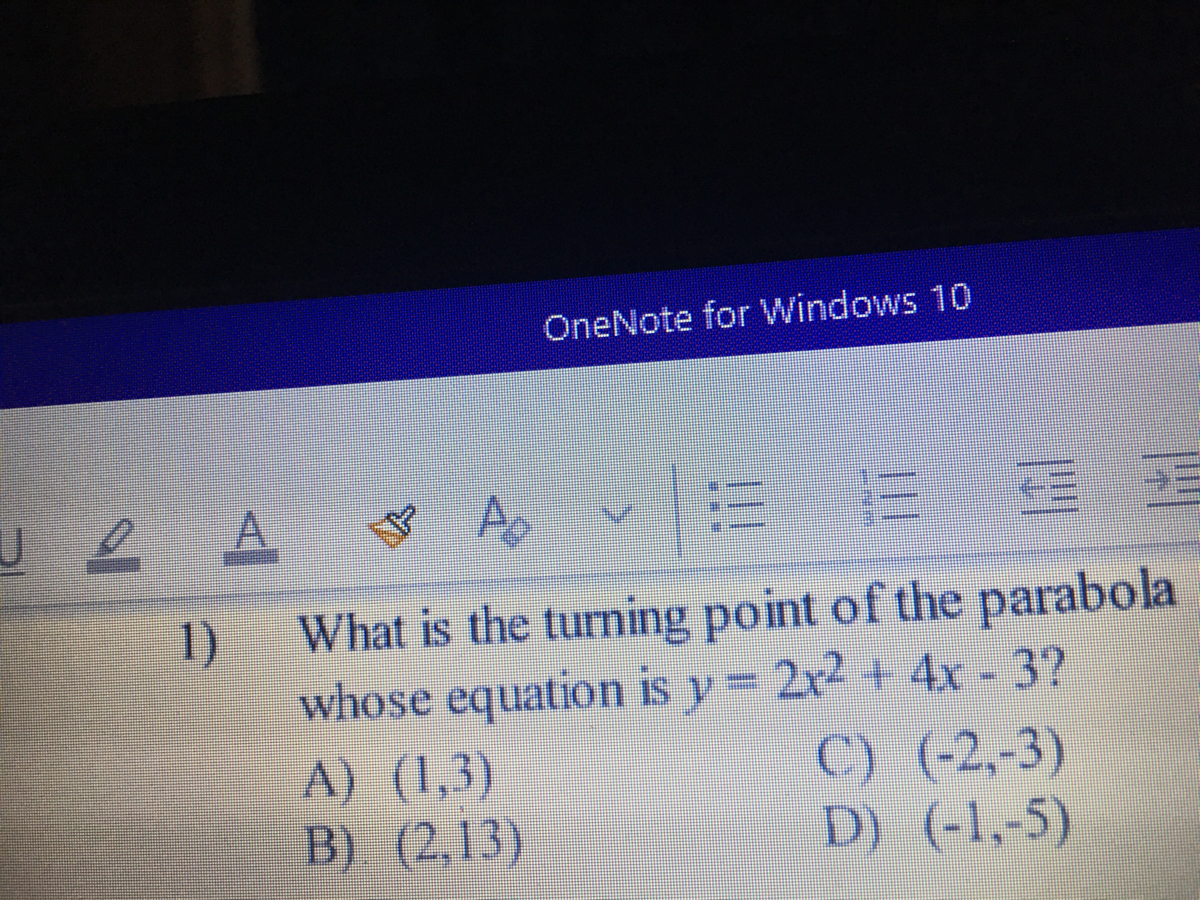



Answered 1 What Is The Turning Point Of The Bartleby
Solved The base of is the region enclosed by the parabola y=1x^2 and the xaxis Crosssections perpendicular to the yaxis are squares SladerIt is easier to plot; Issuu is a digital publishing platform that makes it simple to publish magazines, catalogs, newspapers, books, and more online Easily share your publications and get



How Do You Graph Y 2x 2 4x 3 Mathskey Com



What S The Axis Of Symetry Vertex And Graph Y 2x 2 6x 1 Mathskey Com
Moltiplichiamo, primo e secondo membro, per 2q 2d, e avremo (2q 2d)a = 1 2qa 2da = 1 Portiamo a secondo membro 2da cambiandogli di segno 2qa = 1 2da Dividiamo entrambi i membri per 2a q = 1/2a d Invece, dalla seconda equazione, ricaviamo la p b = 2paSigue primero el orden de las operaciones antes de mover el resto de los números al otro lado Deja la b en un lado de la ecuación para resolverla En el ejemplo, la fórmula ha quedado como 8 = 1 (3)b Multiplica 1 y 3 para obtener 8 = 3b Debido a que 3 es un número positivo, resta 3 en cada lado para aislar a bY^ {2}2xyx^ {2}=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y=\frac {2x±\sqrt {\left (2x\right)^ {2}4x^ {2}}} {2}




Graphing Parabolas



Draw The Graphs Of The Quadratic Polynomial F X 3 2x X 2 Sarthaks Econnect Largest Online Education Community
SOLUTIONS Problem 1 Find the critical points of the function f(x;y) = 2x3 3x2y 12x2 3y2 and determine their type ie local min/local max/saddle point Are there any global min/max?ESERCIZIO 1 Scrivere l'equazione della retta tangente al grafico della funzione ( ) = = y f x x e x−3 2 2 nel punto di ascissa x 0 =1 SOLUZIONE calcolo 0 = y f x 0 ( ) 0 =y f =(1) 1 calcolo ′f x 0 ( ) ′ =( ) 3 −2 2 2 2 f x x e x e x −3 2 2 ⇒ f′ =(1) 5 la retta tangente ha equazione = ′ 0 − ( )( ) y f x x x y 0 0, ovvero è la retta passante per Persamaan terakhir adalah persamaan garis lurus yang melalui dua titik, yaitu A (x fi, y 2) dan B (x 2, y 2 ) Perhatikan kembali rumus (4), rumus tersebut dapat diubah menjadi Ingat bahwa 4 2 —4 fi = m Jadi, ı2—ıfi y — y fi = m (x — x fi) Rumus tersebut adalah untuk menentukan persamaan garis lurus yang gradiennya m dan



Mathscene Functions 1 Lesson 3



Quadratics Graphing Parabolas Sparknotes
Step 1) Find the vertex (the vertex is the either the highest or lowest point on the graph) Also, the vertex is at the axis of symmetry of the parabola (ie it divides it in two) Step 2) Once you have the vertex, find two points on the left side of the axis of symmetry (the lineDx = " x5 15 − x8 24 # 2 0 = 32 15 − 256 24 = − 128 15 07 Example Evaluate Z π π/2Explicación de la forma de graficar y encontrar la ecuación canónica de la parábola cuando se conocen las coordenadas de el foco y la ecuación de la directri
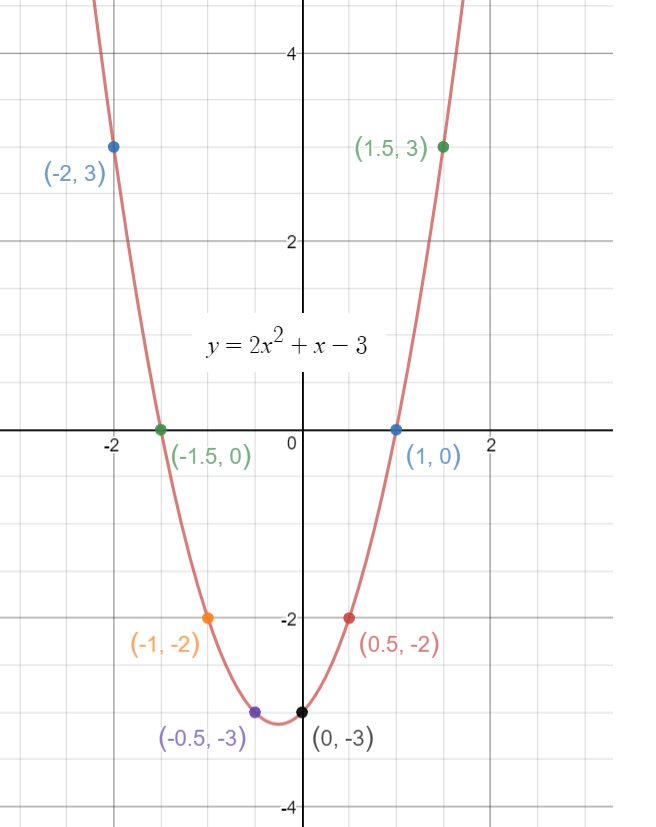



How To Do You Graph Y 2x 2 X 3 By Plotting Points Socratic



Solution Y 3 2x 1
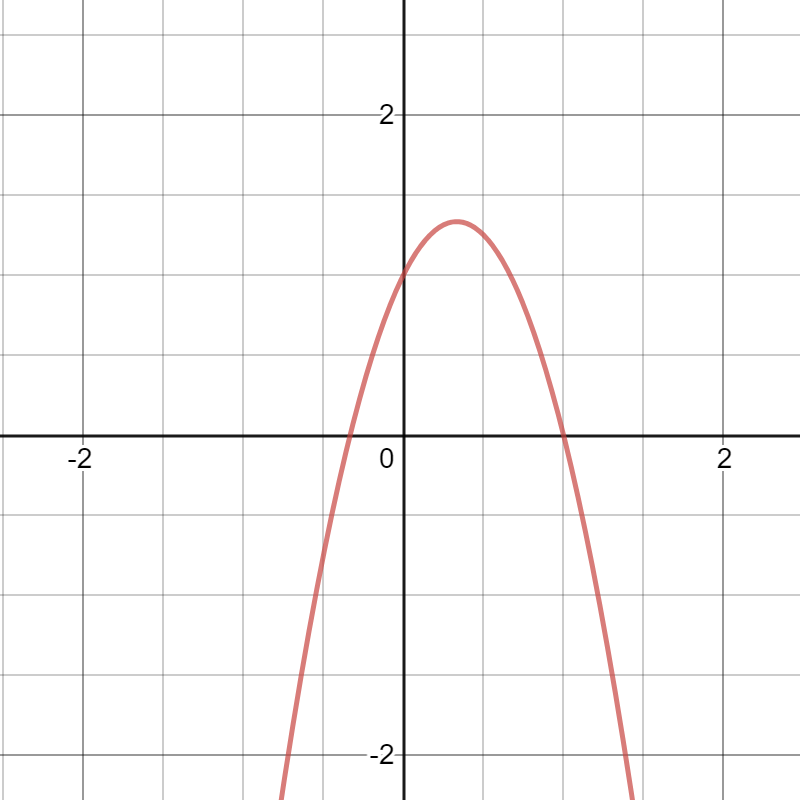



Forms Of Quadratics Explanations Tips And Examples Albert Resources




Solution Find The Equation Of The Axis Of Symmetry Of The Function Y 2x 2




Answered What Is The Turning Point Of The Bartleby



Graphing Quadratic Functions
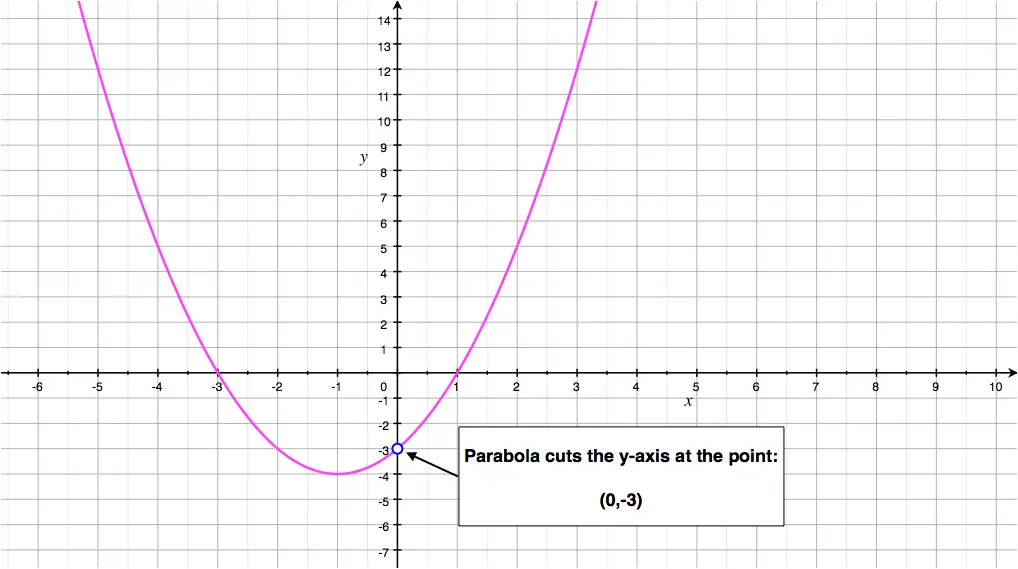



Quadratic Function Parabola




Find The Axis Of Symmetry 1 And The Vertex 2 Of A Parabola Ppt Download
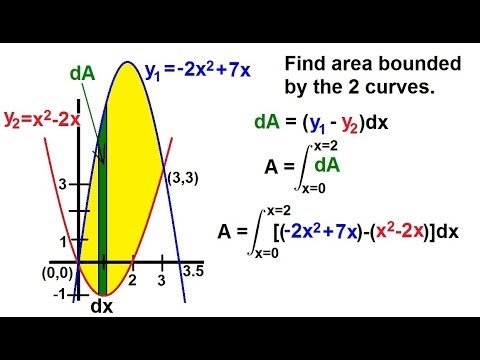



Calculus 2 Integration Finding The Area Between Curves 2 Of 22 Ex 2 Y X 2 2x Y 2x 2 7x Youtube



View Question At What Point Does The Line Normal To Y 3 2x 3x 2 At 1 8 Intersect The Parabola A Second Time



Solved At What Point On The Parabola Y 3x 2 2x Is The Tangent Line Parallel To The Line Y 10x 2 Course Hero



Find The Focus Vertex Directrix Domain Range And Graph The Parabola Of Y 3 2x 2 Mathskey Com



Parabola Questions And Problems With Detailed Solutions



Instructional Unit The Parabola Day 4 And 5
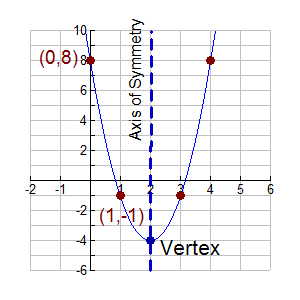



Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math



4 Graph Of The Quadratic Function



Www Nrcs Net Downloads T7 2 hw odds and evens3 Pdf




Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




Ex 6 3 15 Find Equation Of Tangent Line To Y X2 2x 7




Question 14 5 Points For The Function Y 3 2x 3 2 4 Describe The Homeworklib
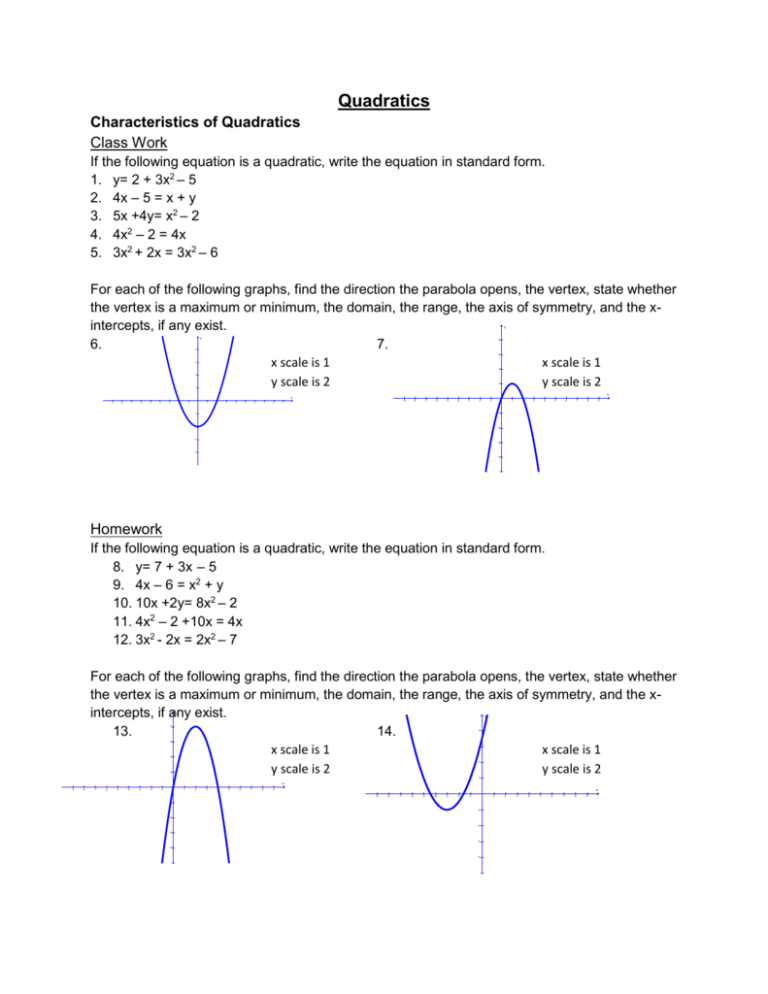



Quadratics
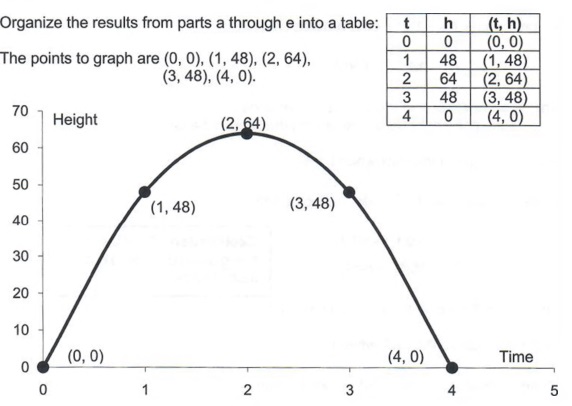



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



Http Www Tippcityschools Com Cms Lib6 Oh Centricity Domain 91 Chapter 10 review ws 1 solutions borchers Pdf



Quadratics
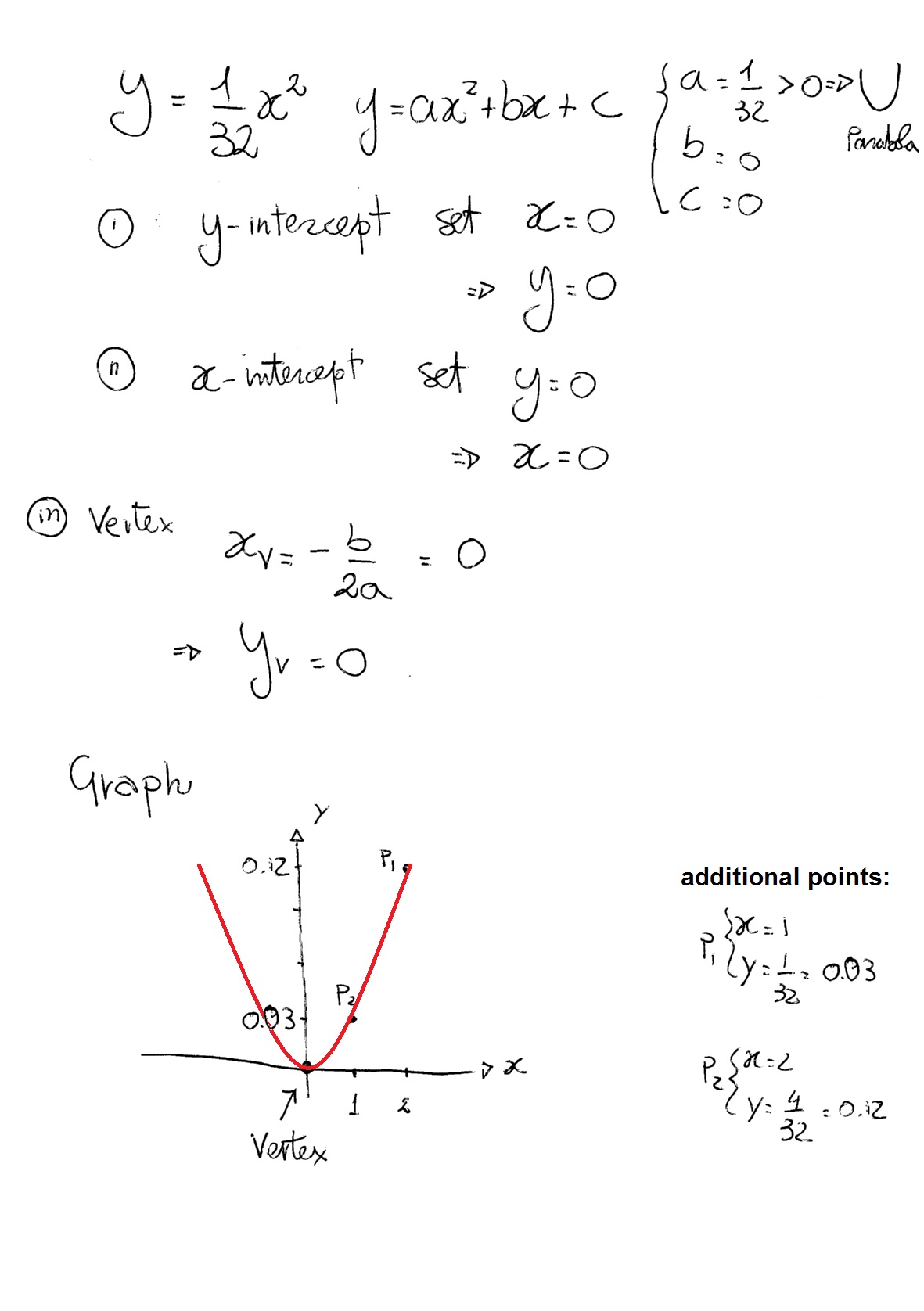



How To Graph A Parabola Y 1 32x 2 Socratic
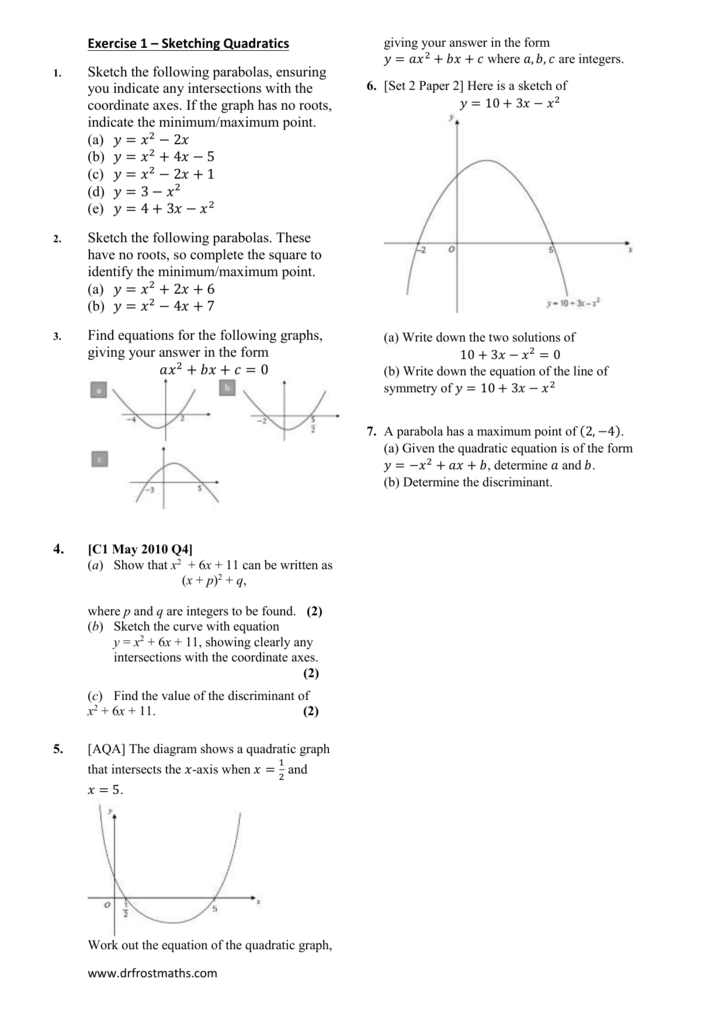



C1 Igcse Further Maths Sketching Graphs Worksheet
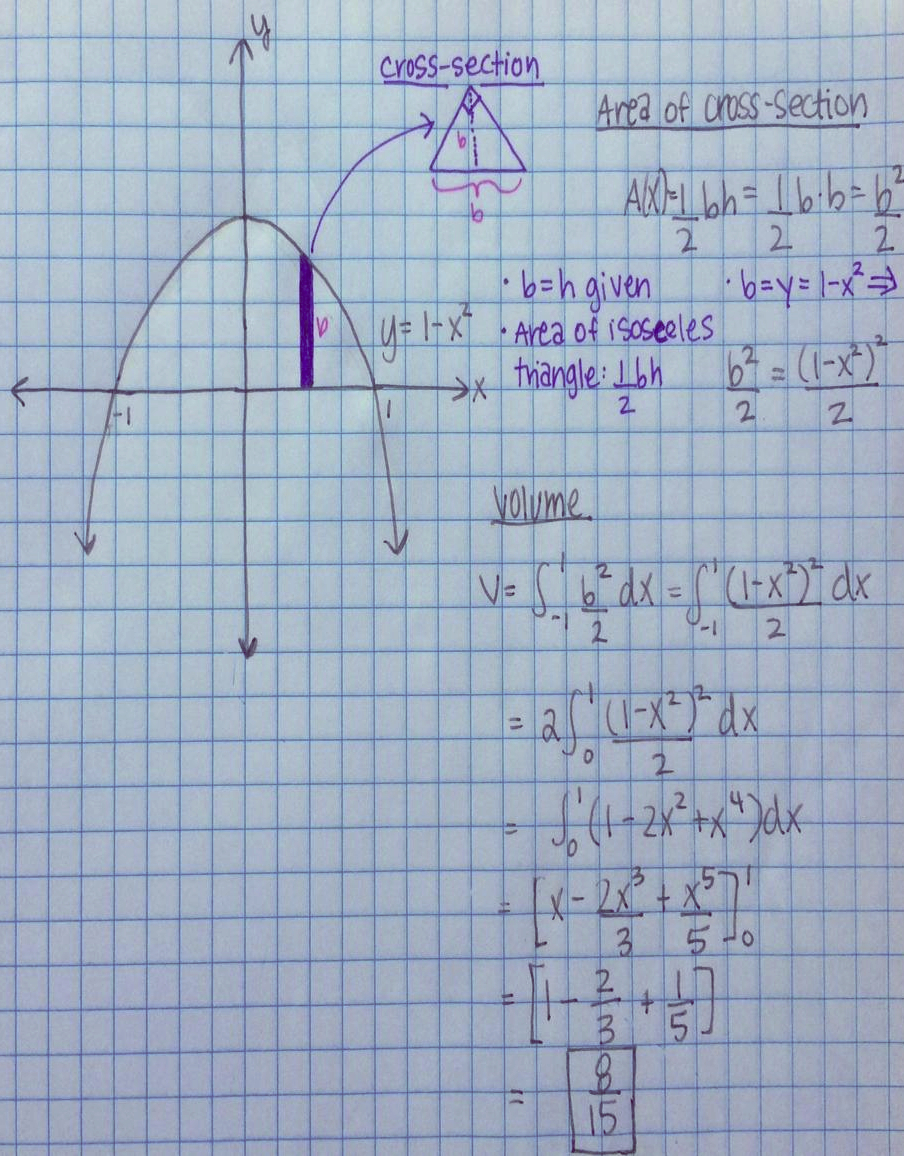



Find The Volume Of The Described Solid S The Base Of Is The Region Enclosed By The Parabola Y 1 X 2 And The X Axis But Cross Sections Perpendicular To The X Axis Are Isosceles Triangles With



Www Sanjuan Edu Site Handlers Filedownload Ashx Moduleinstanceid Dataid Filename Module 6 review answers Pdf




Vertex Form Vertex Form Vertex Form Is Another



Www D105 Net Cms Lib Il Centricity Domain 610 Vertex practice worksheet answers Pdf




Draw The Graphs Of The Quadratic Polynomial F X 3 2x X 2



Quadratics Graphing Parabolas Sparknotes




Draw The Graphs Of The Quadratic Polynomial F X 3 2x X 2



Untitled Document




Use The Parabola Tool To Graph The Quadratic Function F X 2x2 32x 126 Graph The Parabola By Brainly Com



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



2



Www Cravenk12 Org Cms Lib Nc Centricity Domain 1711 Unit 2 test quadratics review Pdf
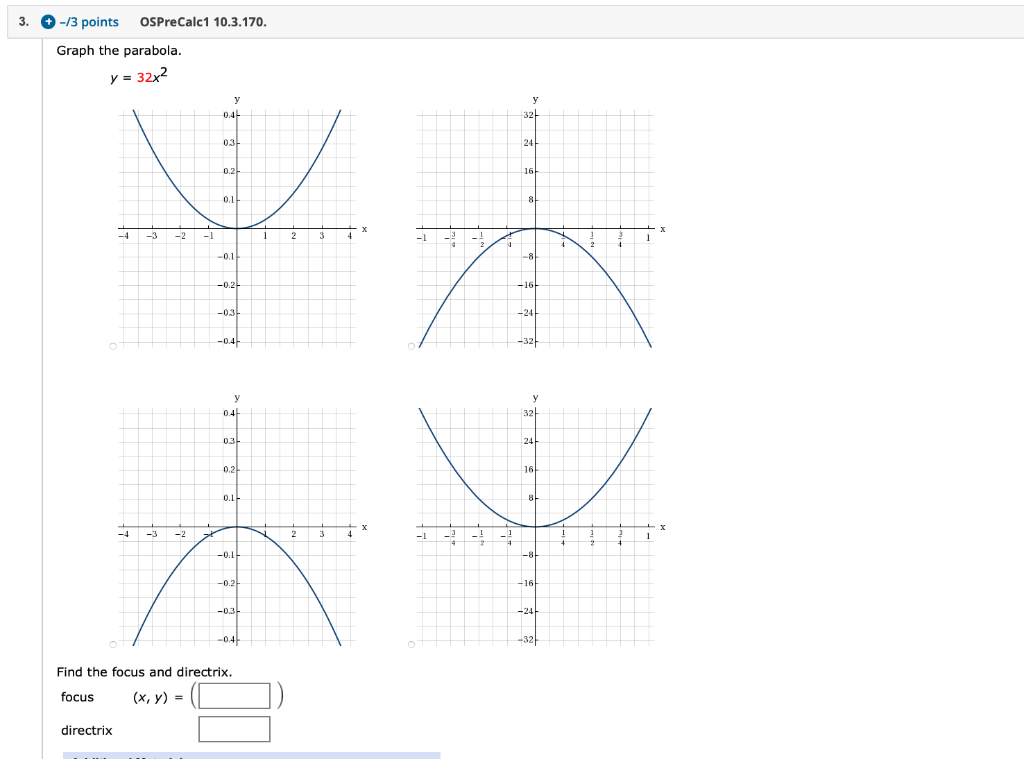



Solved 5 1 Points Osprecalc1 8 6 405 Parameterize Chegg Com




Warm Up For Lesson 3 6 Identify The Vertex Of Each Parabola 1 Y X 3 2 5 2 Y 2x 2 7 3 Y 3 X 1 2 4 4 Y 5 X 4 2 5 Ppt Download



Www Cravenk12 Org Cms Lib Nc Centricity Domain 1711 Unit 2 test quadratics review Pdf




Quadratic Functions Functions Siyavula



1



Double Integrals Over General Regions Page 2



Math Scene Equations Iii Lesson 3 Quadratic Equations
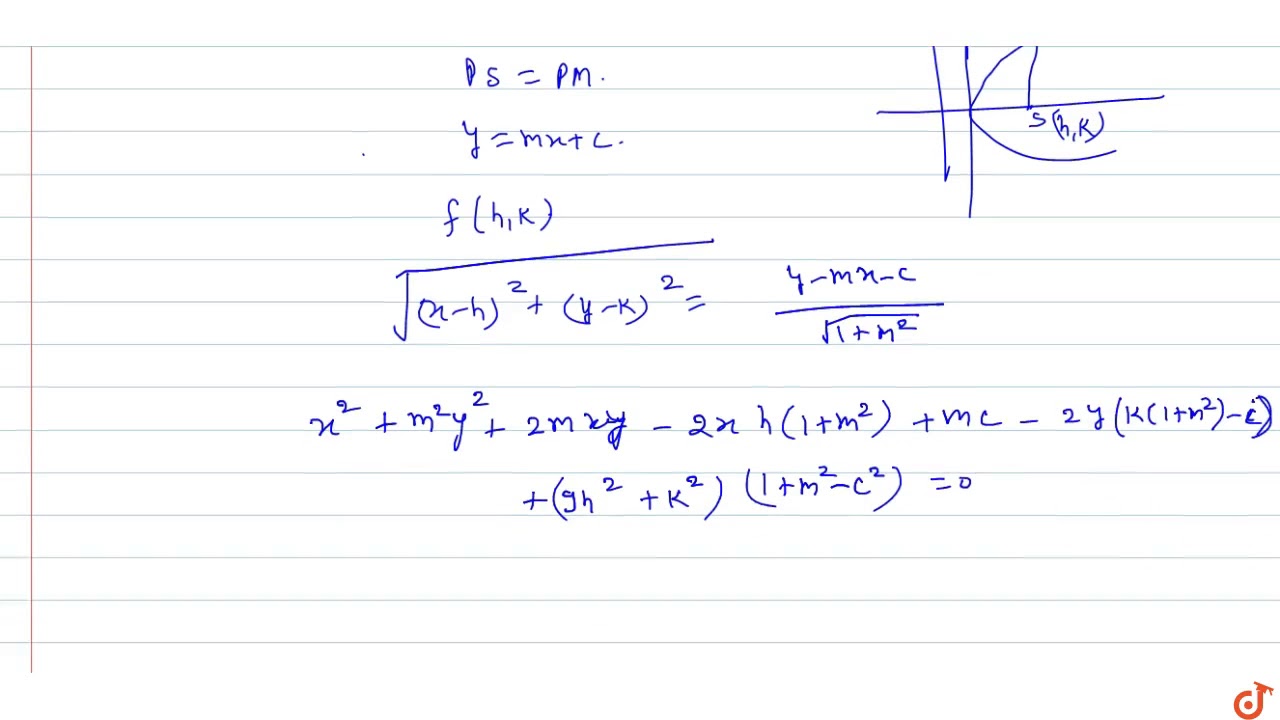



For Parabola X 2 Y 2 2x Y 6x 2y 3 0 The Focus Is Youtube




Bingo Graphing Quadratics Parabolas In Vertex Form By Algebra Made Fun
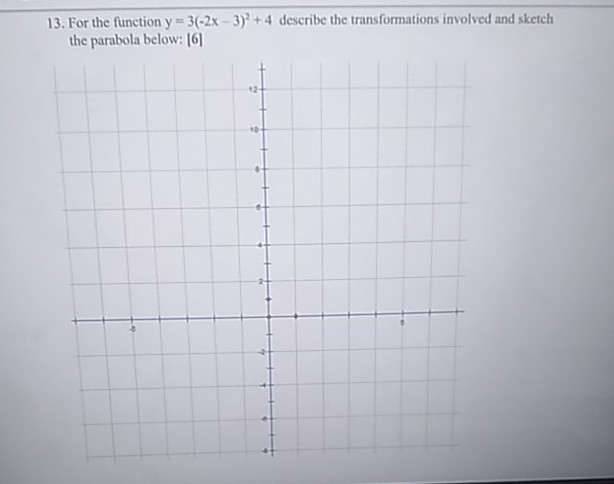



13 For The Function Y 3 2x 3 2 4 Describe The Chegg Com
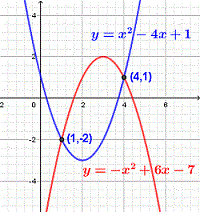



Parabola Questions And Problems With Detailed Solutions



How To Find The Focus Of The Parabola X 2 4xy 4y 2 32x 4y 16 0 Quora



The Quadratic Function




Graph The Parabola And Give Its Vertex Axis X Intercepts And Y Intercept Y 2x 2 8x 16 Study Com



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic



What Is The Angle Between The Lines 2x Y 3 0 And X Y 2 0 Quora



Solved Ned By The Equation X 3 2 Y 2 2 25 Which Shape Is Defined By The Equation Y 2x 2 3 Which Shape Is Defined By The Equation Course Hero




Draw The Graph Of Polynomial F X 3 2x X2 Brainly In



Quadratic Functions




The Parabola Algebra And Trigonometry
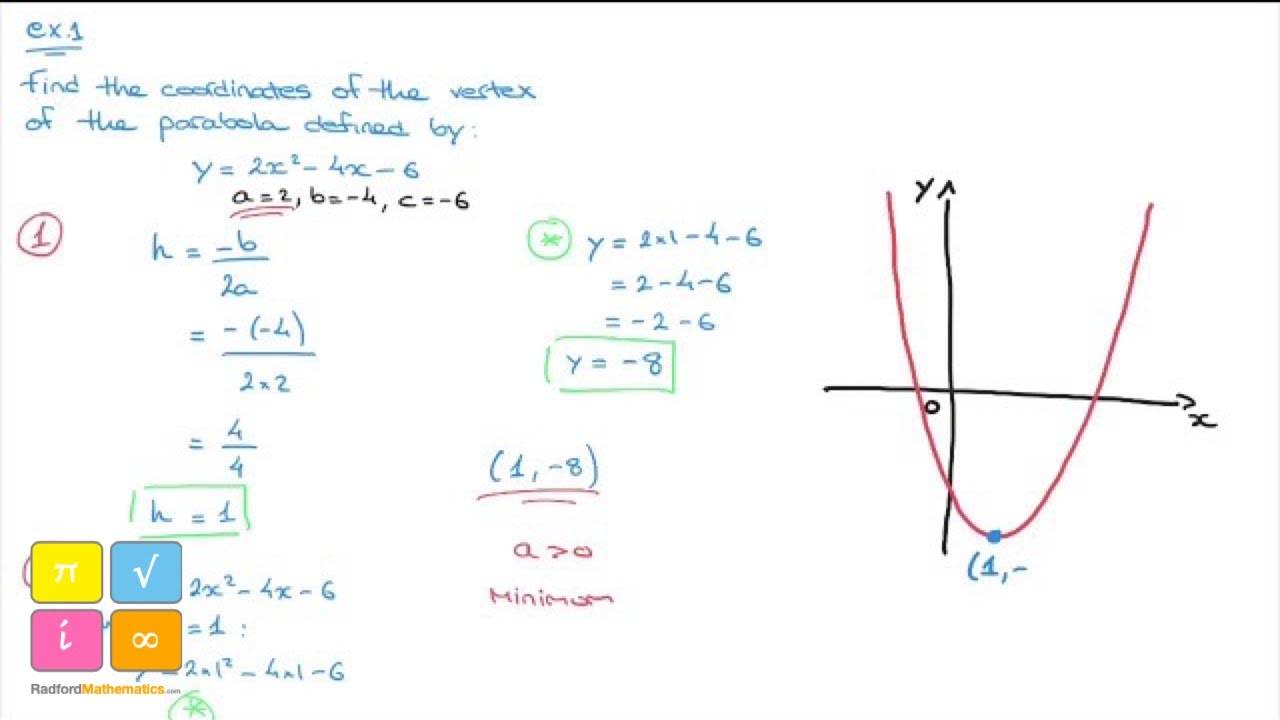



Quadratic Function Parabola



1
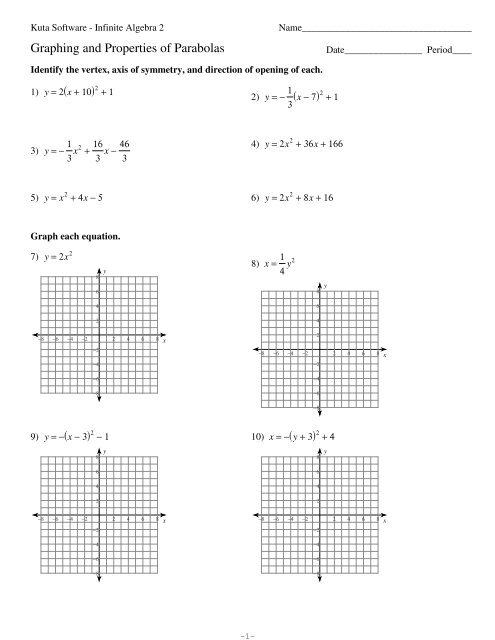



Graphing And Properties Of Parabolas



Quadratics
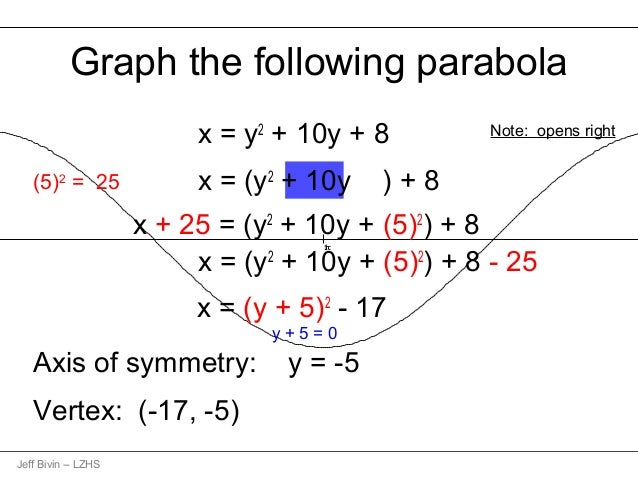



Parabola
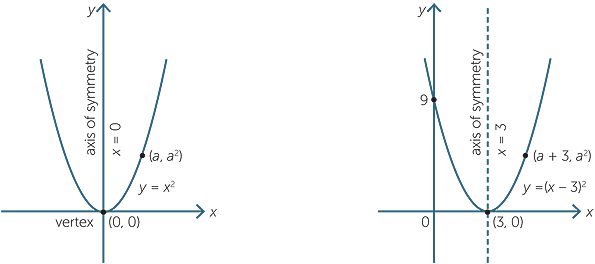



Quadratic Function



How Many Times Does The Graph Of Y 2xsquared 2x 3 Intersect The X Axis Math Central



Graphing Types Of Functions




Find The Point On The Parabola Y 2 2x Which Is Closest To Th




Which Equation Matches The Following Parabola K Y Gauthmath



How Do You Graph Y 2x 2 4x 3 Mathskey Com



Solution I Have To Find The Vertex Axis Of Symmetry Minimum Or Maximum Value And Range Of The Parabola The Formula Is Y Ax 2 Bx C Question Y 2x 2 6x 3 What I Have So Far Y 2x 2 6x



Quadratic Functions




The Slope Of The Normal To The Curve Y 2x 2 3sin X At X 0is




Graphing Parabolas



1




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy




Find The Volume V Of The Described Solid S The Base Of S Is The Region Enclosed By The Parabola Y 3 2x2 And The X Axis Cross Sections Perpendicular To The Y Axis



Mathscene Functions 1 Lesson 3
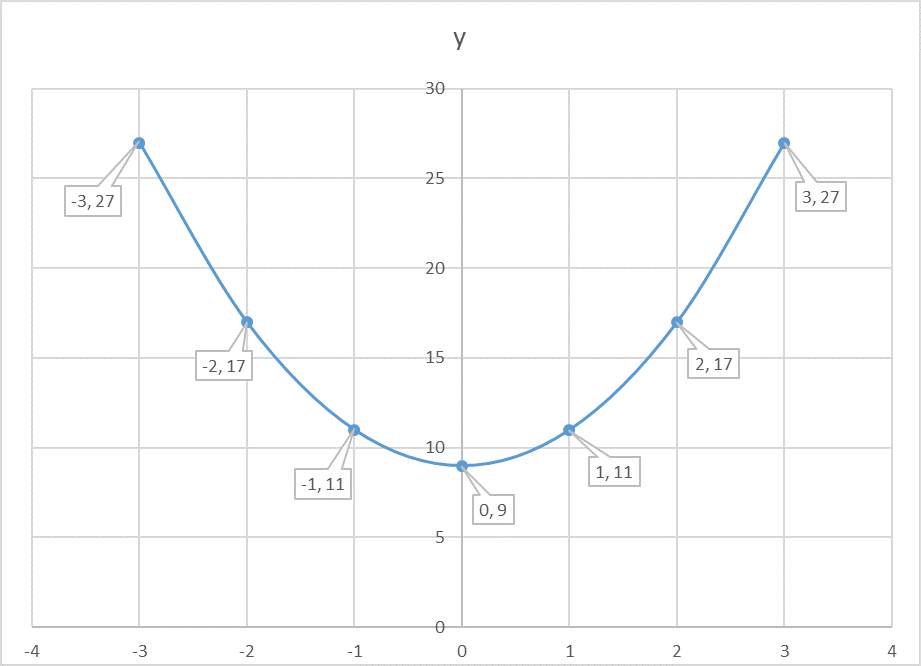



How Do You Graph The Parabola Y 2x 2 9 Socratic



1




Mfg The Vertex Of A Parabola



Solution Graph The Parabola Y 3 2 X 2
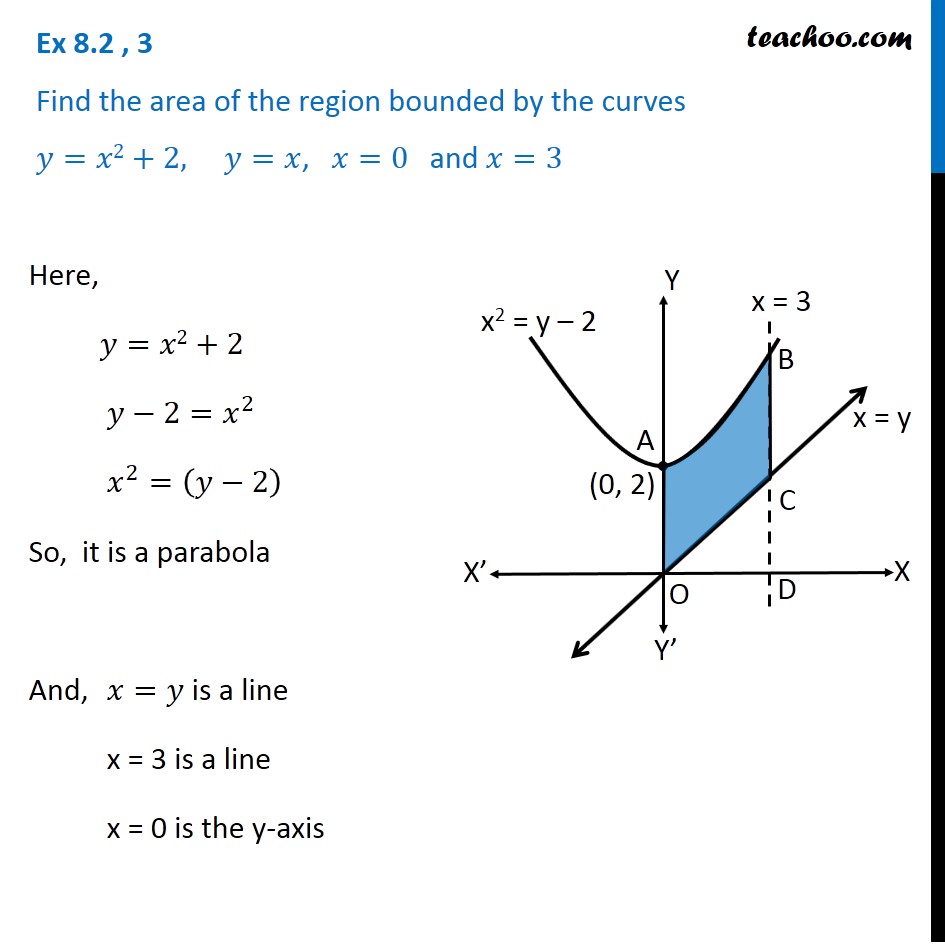



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



Parabolas



0 件のコメント:
コメントを投稿