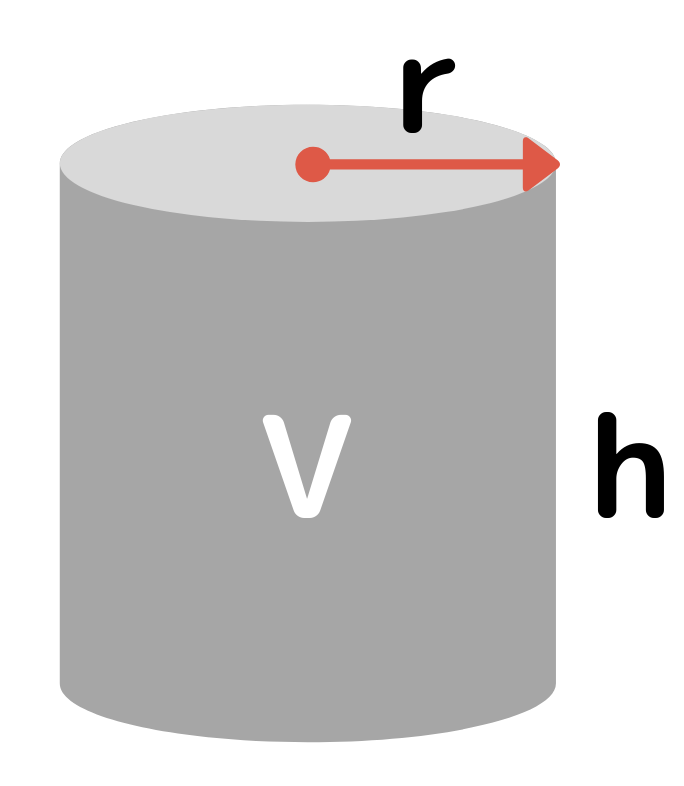
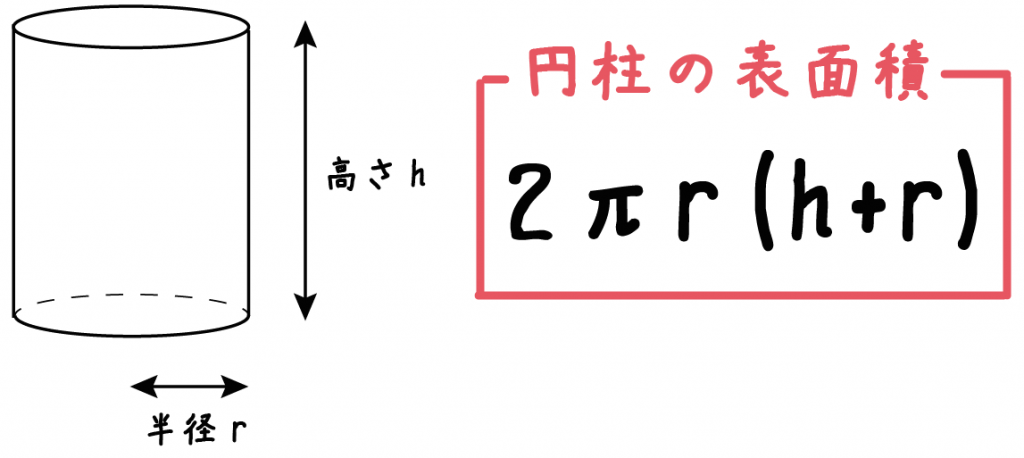
ア(ア)基本的な角柱及び円柱の体積の計算による求め方について理解すること。 イ(ア)図形を構成する要素に着目し,基本図形の体積の求め方を見いだすとともに,その表現を振り返 り,簡潔かつ的確な表現に高め,公式として導くこと。 児童はこれまでに,面積や体積の測定の意味や 円柱の表面積の求め方の公式 をつかってしまえば2秒ぐらいで計算できちゃうんだ。 下の図のように、円柱底面の半径をr、高さをhとすると、 2πr(hr) 《円柱の体積の求め方》 この円柱の底面は、半径が8cmの円なので 底面積=8×8×314=096(㎠) 求める円柱の体積=底面積×高さ=096×10=096(cm³)

体積 表面積
円柱 展開図 体積 求め方
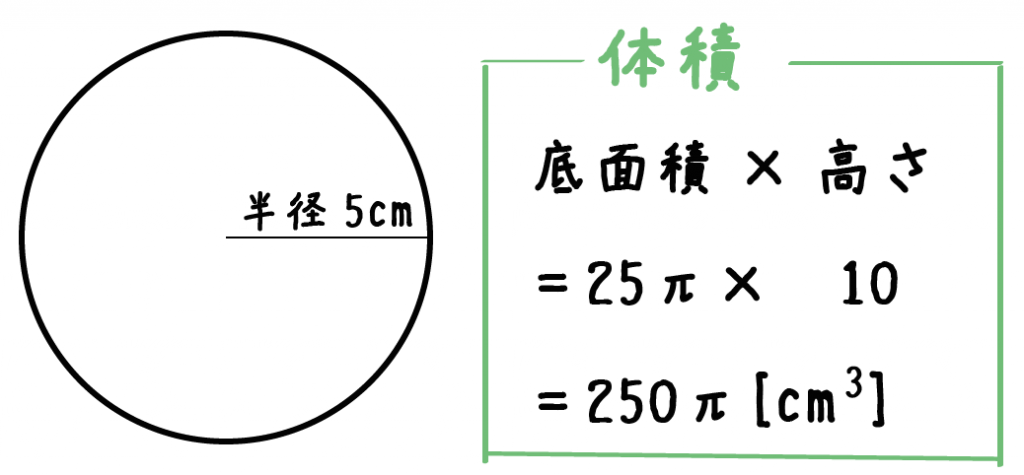
円柱 展開図 体積 求め方- 円柱の体積求め方(小学生) 次の円柱の体積を求めましょう。 それでは、公式通り考えてみましょう。 まずは底面積を求めます。 半径が6㎝なので $$6\times 6\times 314=(cm^2)$$ となりますね。 (ちょっと数字がデカいな(^^;) 底面積が求まれば、あとは高さをかけるだけ! $$\Large{\times 8 RCCYLINDERカスタムワークシート関数群は、直円柱の体積や表面積などを計算します。 直円柱とは、正円を底面とした筒状の立体です。 RCCYLINDERカスタムワークシート関数群には、下記の関数が含まれます。 ワークシート関数だけで (VBAを使用せずに)同じことをしたい場合は コチラ の記事を参照して下さい。 関数名 機能 関数名の由来 RCCYLINDERSUR 直円柱の半径と




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。 覚え方は、『3分で忘れる心配あーるの参上。円柱の体積 V は、 円周率× 半径 × 半径 × 高さ角柱や円柱の体積に関心をもち,それらの体積の求め方を考え,公式を導き出そうとしている。 (算数への関心・意欲・態度) 角柱や円柱の体積を既習の立体に帰着させたり,底面の面積を基にしたりして,体積の求め方を考えて いる。 (数学的な考え方)
円柱・円筒の体積計算フォーム 円柱・円筒の直径cmと高さhcmから体積Vリットルを計算できます。 計算式 Vリットル=(π×r×r×h)/1000数学的な考え方 角柱や円柱の体積の求め方について,直方体の体積の求め方から類推し,考える ことができる。 技能 角柱や円柱の体積を,公式を用いて求めることができる。 知識・理解 角柱や円柱の体積は,底面積×高さで求められることを理解する。 3単元と児童 (1)単元について 児童はア 角柱および円柱の体積の求め方を考えること。 直方体,立方体の場合の体積の求め方をもとにして,これらの立体の体積も計算によって求める ことができることを理解することが主なねらいとなっている。 本単元では,求積公式を覚えて体積を求められればよいのではなく,どのように
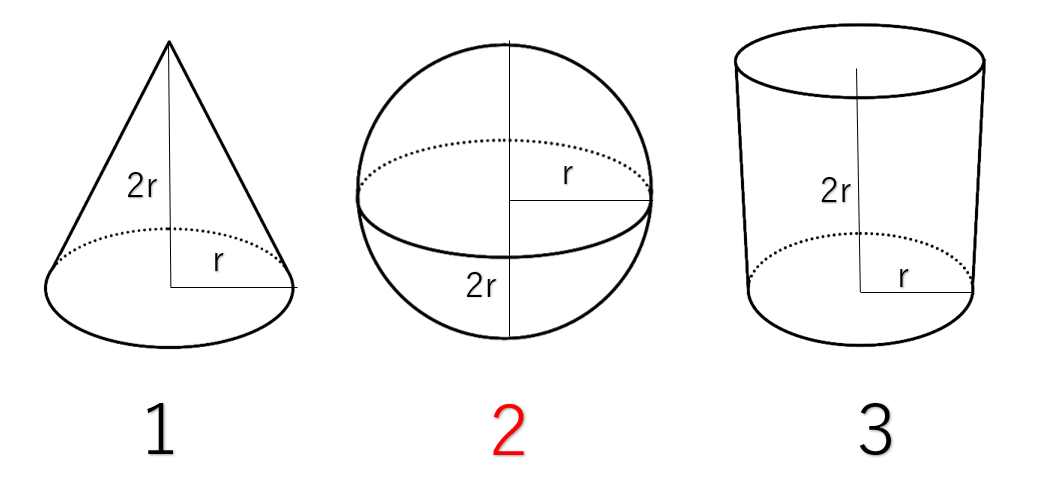
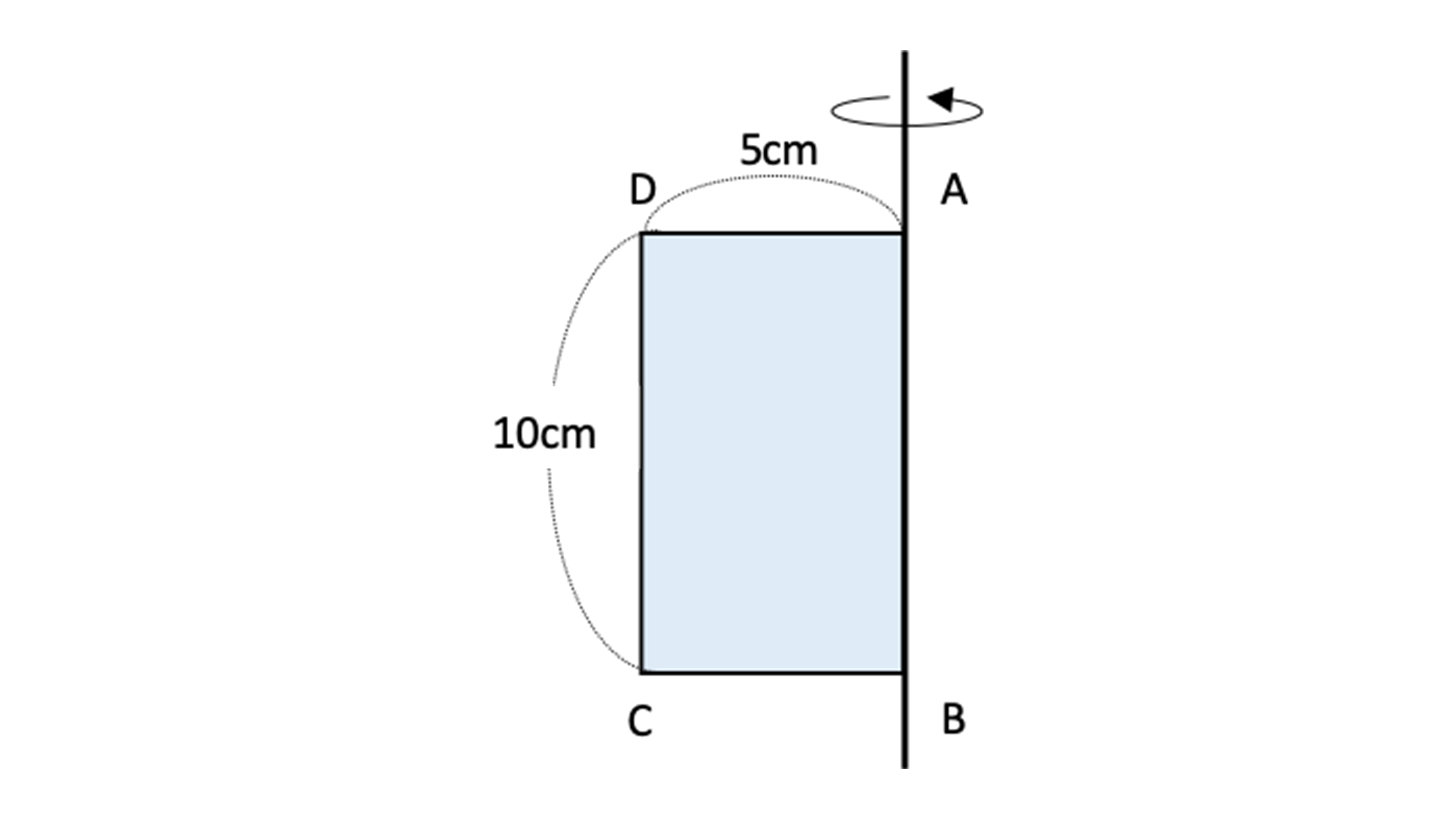
直方体の体積 H: S: 体積: 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい 四角すい角柱や円柱の体積の求め方を公式化した過程を振り返り,体積の求め方について多面的に捉え,検 討してよりよいものを求めて考えるとともに,数学のよさに気付き,学習したことを今後の生活や学 習に活用しようとする態度を養うようにする。 3 単元観 本単元は,小学校学習指導要領算数科この円柱において, 底面の面積は,π×22=4π(cm2), 高さは2cmなので, 円柱の体積=底面の面積×高さ より, 体積は,4π×2=8π(cm3)となります。 このように,回転体の体積を求めることは中学1年で学習しますが,上の方法とまったくちがう求め方があ ります。その方法を紹介しましょう。 下




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋
体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方立体の体積 体積ボタン 解説 体積ボタン2 解説 立体(L字型) 解説 6年 分数のかけ算とわり算 解説 図形・円と直線の関係 解説 比例 解説 比例と反比例① 解説 比例と反比例① v2 解説 比例と反比例② 解説 変化する2つの量 解説 割合を使って円柱の体積を求める公式は、次の通りです。 V = Sh = πr2h V = S h = π r 2 h ここで、V は円柱の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。



円柱の体積の計算フォーム 直径 高さ Cm 体積 リットル を算出 寝袋 シュラフのプロが極秘で教える 失敗しない選び方 使い方
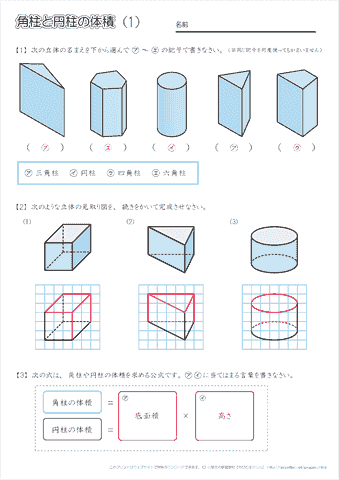



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
円柱の体積は 半径×半径×π×高さ ですので、ここでは、 r×r×π×2r=2πr 3 ですので球の体積は、 2πr 3 ×2/3= 4/3πr 3 ということで、公式がでましたね! 理解できたでしょうか。 以上が、国分寺、小平の個別指導塾、こいがくぼ翼学習塾から、球の体積の求め立方体 直方体 断面積から体積計算 公式 求め方 高さ 底面積 自動 volume 断面積から体積 立方体 直方体 面積;体積を求めるときのポイントは どのような面が集まって立体を形成しているか をイメージすることが大切です。 円柱 下の図のように半径\(R\)高さ\(h\)の円柱の体積\(V\)を求めてみたいと思います。 まず円柱を薄切りにした円を考えてみます。そうすると
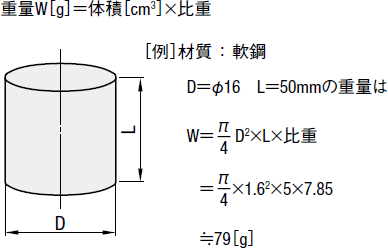



体積 重量の求め方 技術情報 Misumi Vona ミスミ
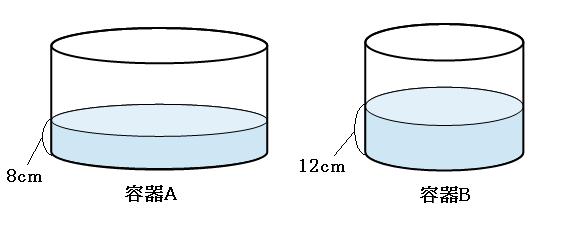



体積と比の問題の解き方 底面積の比と深さの比は逆になる
公式一覧立体の体積・表面積の求め方(円柱・三角柱・円錐・三角錐・球) 体積の公式は何種類もあってわけわからなくなってしまう子が多いです。 ですが、仕組みを知ってしまえば無理して覚えずとも解くことができます。 まずはそれぞれ体積を求めるDvの計算法-ヤコビアンを使うやり方関連ページ ある座標系を他の座標系へ変換するときに関数行列式をいうのを用います。 この時の関数行列式をヤコビアンと呼びます。 このヤコビアンを使って実際にデカルト座標系から極座標、さらには円柱座標系直方体の体積の求め 方から,角柱や円柱の体 積の求積公式を考えて いる。 角柱や円柱の求積公 式を用いて,体積を求め ることができる。 角柱や円柱の体積は, 底面積×高さで求めら れることを理解してい る。 情報の収集 整理・分析 課題の設定 二 既習事項の理解を深める。 (1) 角柱や




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
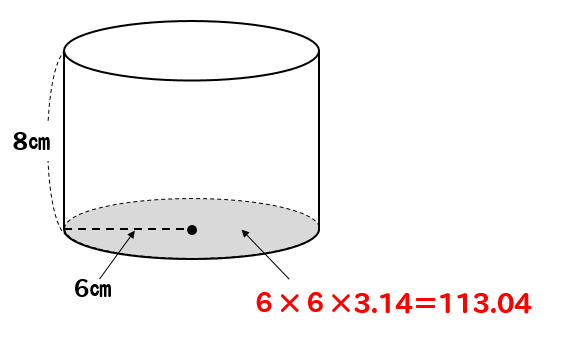
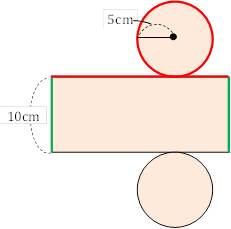
円柱の体積の求め方は、底面積×高さ であることを教えます。 円柱の体積=底面積×高さ 声に出して覚えよう 問題 下の図の円柱の底面の直径は8㎝で、高さは、10㎝です。この円柱の体積を求めましょう。 よくある間違い その1 底面積×高さ =10×10×314×10 体積・表面積の公式や求め方、単位あり計算問題 21年2月19日 この記事では、「円柱」の公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 また、リットルなどの単位を含む計算問題なども紹介していきますので、この「三角すい・四角すいの体積」について詳しく知りたい方はこちら 2 円柱の体積を求める問題 問題1 図の円柱の体積を求めなさい。 問題の見方 立体の体積を求める公式より、~~柱とつく立体の場合, (底面積)×(高さ)=(体積) で求められますね。




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題
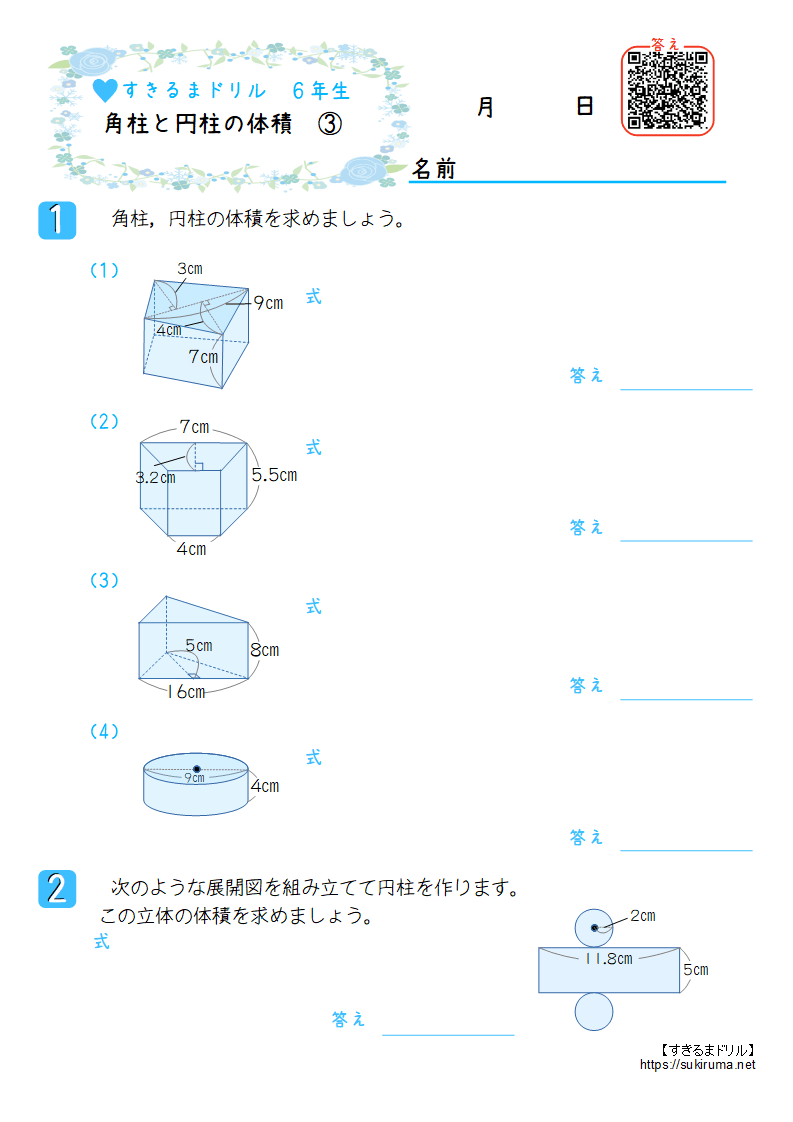



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント
円柱 複合図形の体積の求め方 図形を分けたり、合わせたりして自分の知っている形にする。 5㎝ 4㎝ 9㎝ 5㎝ 4㎝ 3㎝ 9 ㎝ 四角柱の底面の形に注目してみると cm 、下底9 、高さ3 平面の台形を高さ4 cm まで積み上げたと考えると の体積=底面積×高さ;の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 (A)図より、底面の円の半径=18/2=9cm 底面積 (S)=9×9×π=81π (〖cm〗^2) 高さ=15cmより、体積=81π×15=1215π (cm3) 答え:1215ℓ




円柱の表面積の求め方 公式と計算例
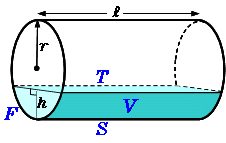



一部が欠けた直円柱の体積 高精度計算サイト
ここでは円柱の体積の求め方を見ていきましょう。 など、つまずくポイントはお子さんによってさまざまです。 長方形の面積は区切りがありますが1つひとつ出さなくても、 1つの長方形として求めれば良いんですよ。 11 体積の公式の一覧 よくつかう体積の公式の一覧を、下記に示します この考え方が、そのまま切頭円柱の体積を求める公式になります。 底面積に異なる高さの平均を掛けると体積が出る。この関係を覚えておいてください。 ちなみに、この考え方は台形の面積を出す公式と実はよく似ています。 上底\(=a\)、下底\(=b\)、高さ\(=h\)という台形があるとしまらくちん設計 com ★重量計算★ -円柱- PR この広告は3ヶ月以上更新がないため表示されています。 ホームページを更新後24時間以内に表示されなくなります。




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
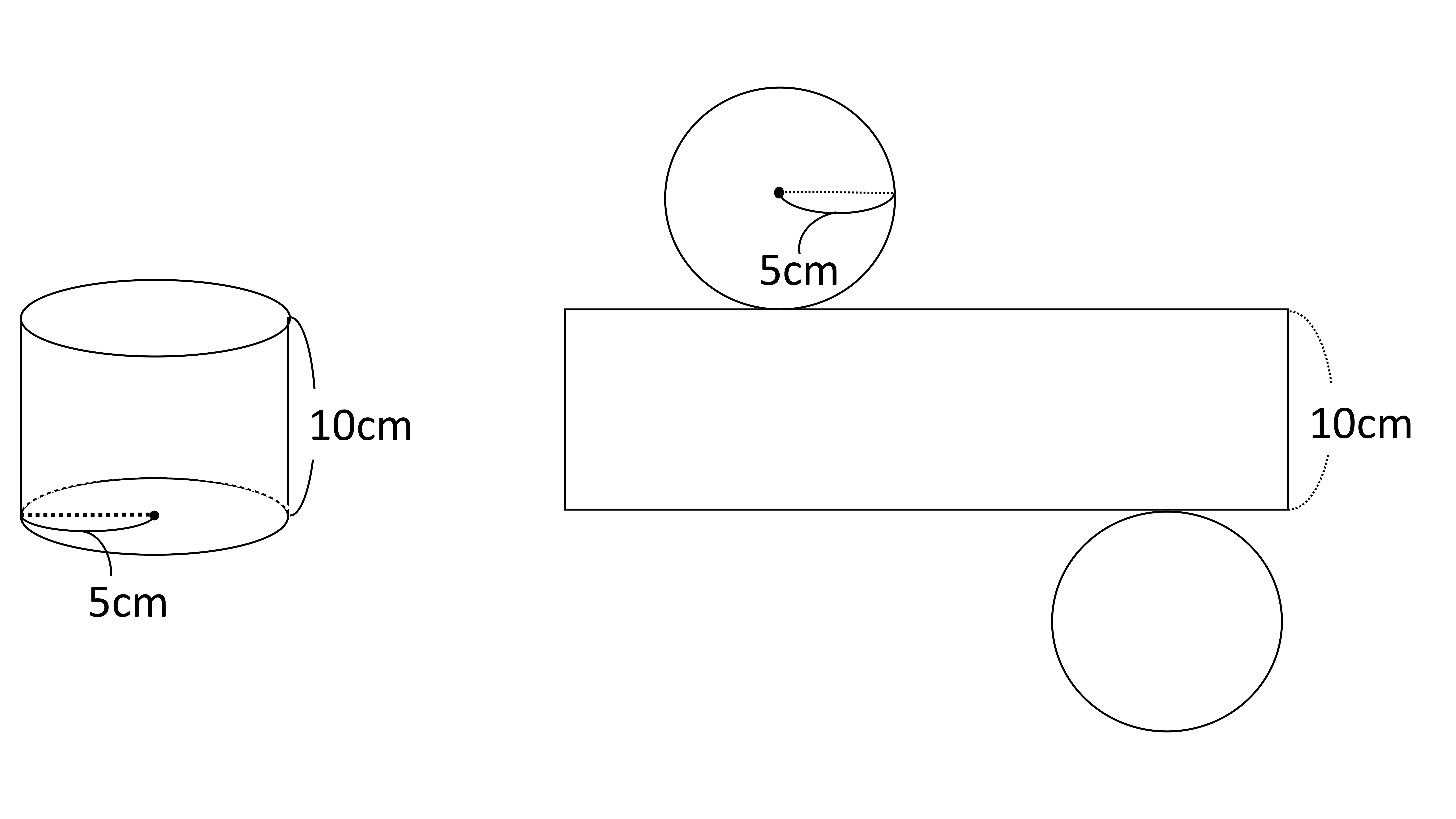
円柱の体積、表面積の求め方はこれでバッチリ!←今回の記事 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!体積は比較的簡単に求めることができると思います。 円柱の体積の公式は V=Sh (Sはもちろんπr2) ですので、これらに問題に指定してある円柱の各数値を代入するだけで求められると思います。 問題は円柱の表面積の求め方です。円錐の表面積や体積の求め方!すぐ分かる方法を慶応生が解説!|高校生向け受験応援メディア「受験のミカタ」 💓 面積と同じように、扇形の弧の長さは「円の直径を出した後、中心角の割合に応じて数字を減少させる」ようにします。 展開したら扇形になる側面の部分と、底の円形の部分
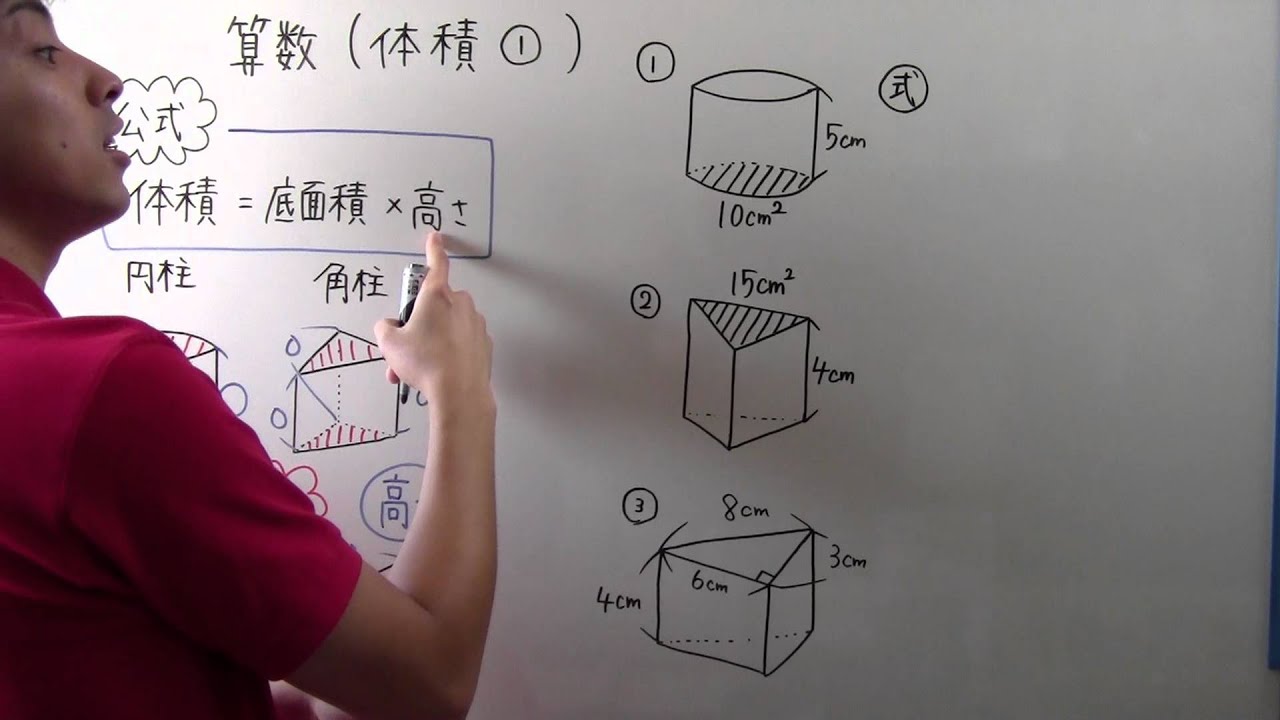



小6 算数 小6 25 体積 円柱 角柱 Youtube




円柱の表面積と体積を求める公式 具体例で学ぶ数学
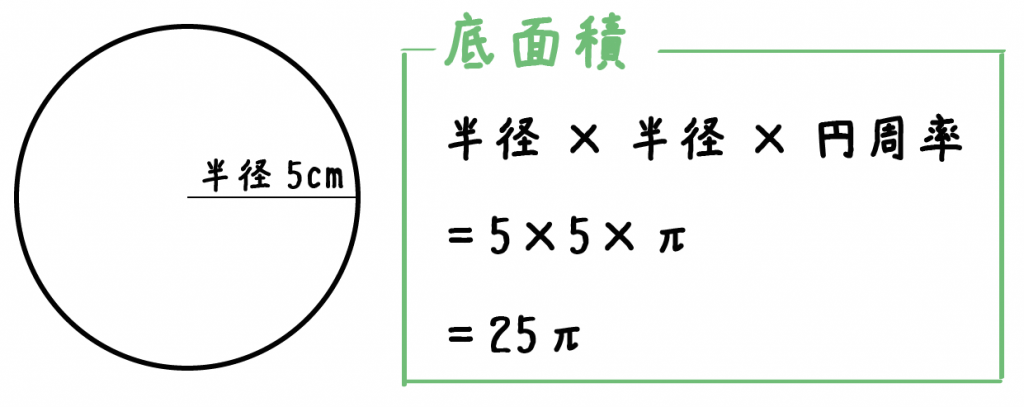
円柱の体積の解説 円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。



Q Tbn And9gcqbxowgsr9fglz9s6nk3xfp1u T2gn5wllytdkpbbfnrgtv43gf Usqp Cau




体積 表面積




球の体積と表面積 公式と計算問題と証明 Irohabook
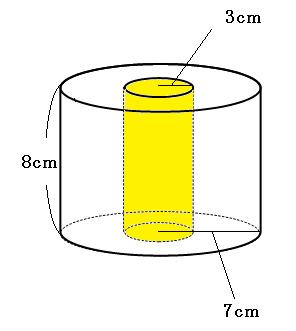



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




体積の求め方 計算公式一覧




円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題



1



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係




角柱 円柱の表面積と体積の公式 数学fun
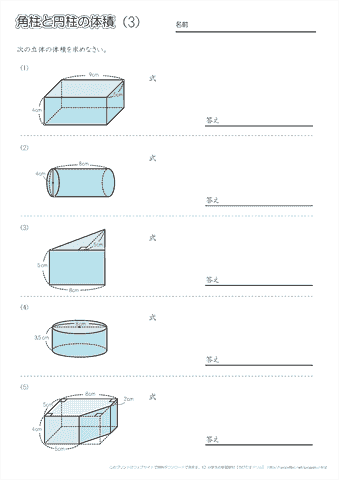



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




円柱の表面積と体積を求める公式 具体例で学ぶ数学
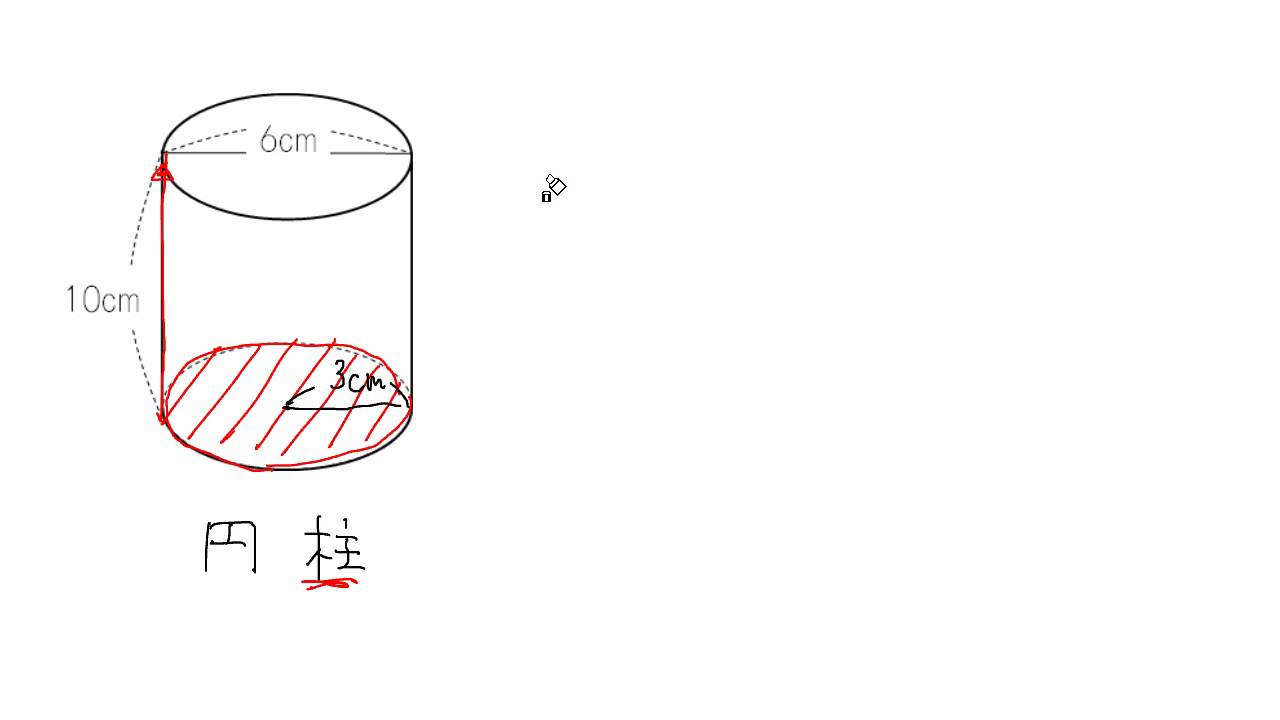



円柱の体積 Youtube



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
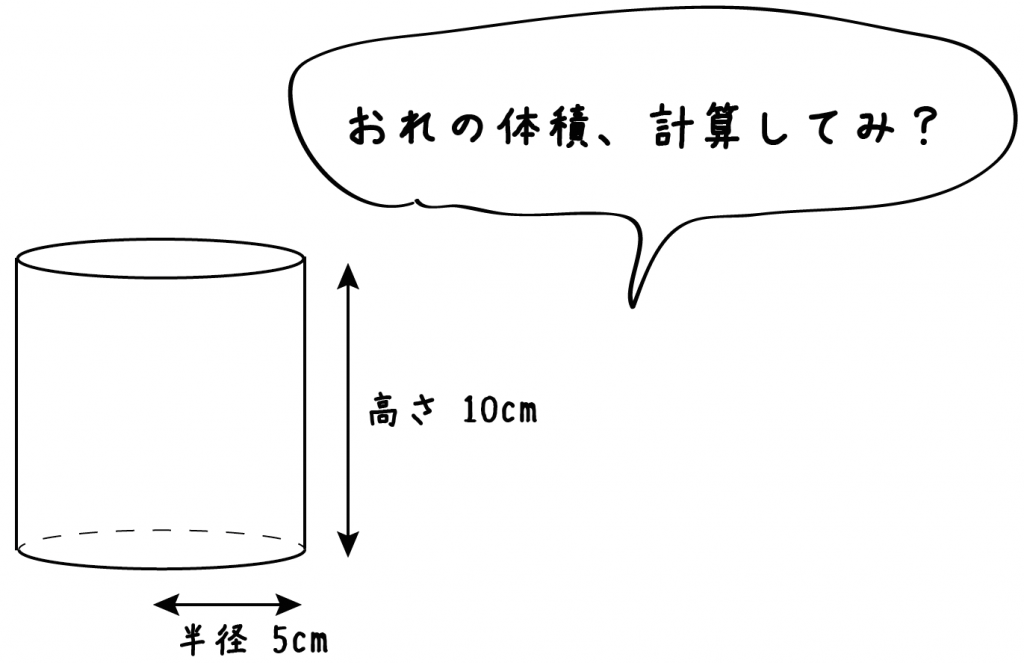



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
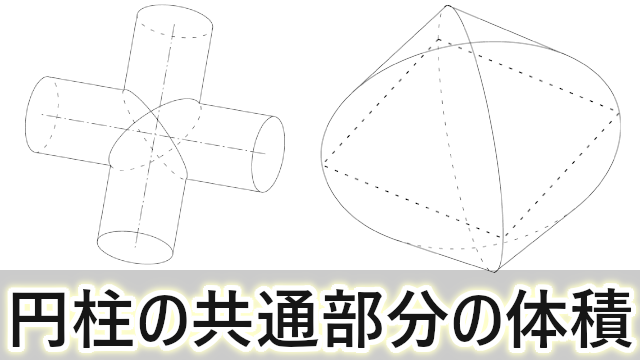



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法



円柱の求め方について なんですが 小学校でやったはずの円柱の体 Yahoo 知恵袋




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の水槽に球を入れる問題 苦手な数学を簡単に



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
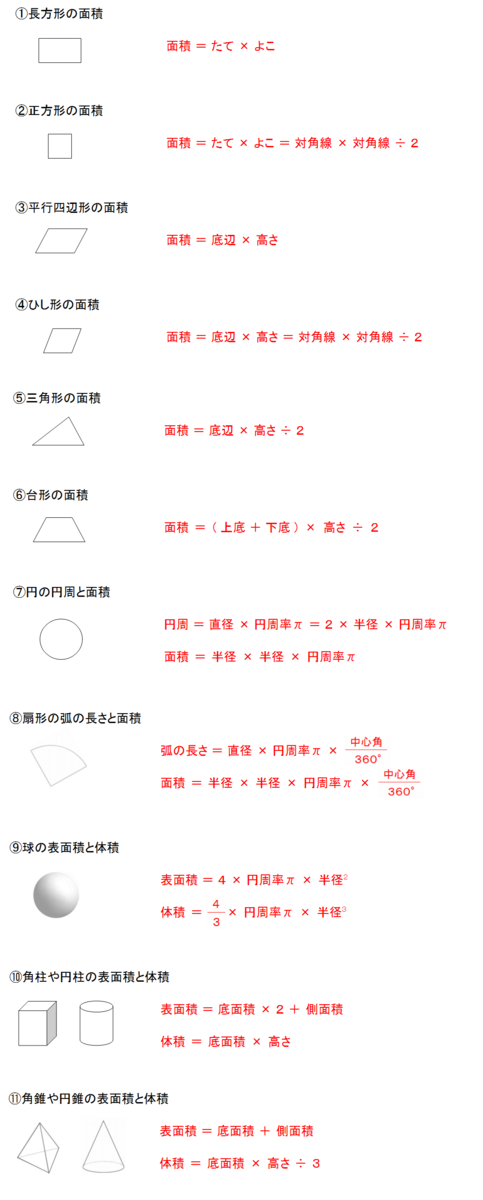



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
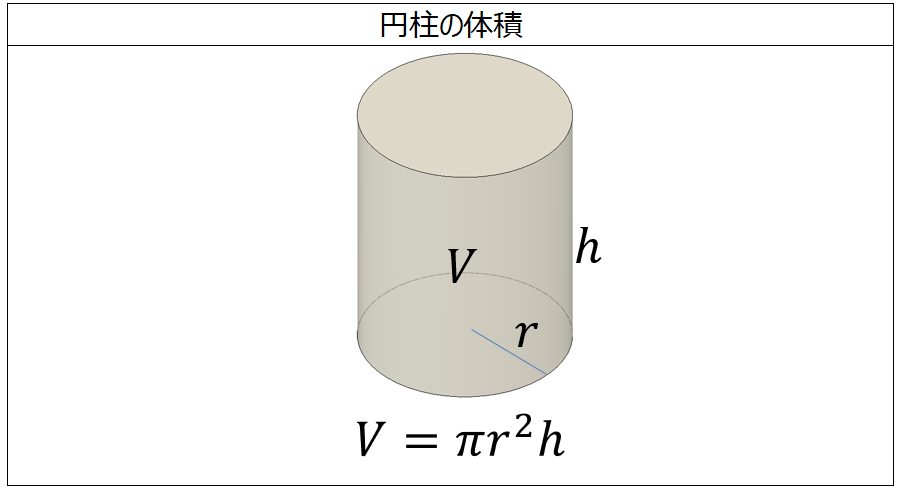



体積の計算 円柱 製品設計知識
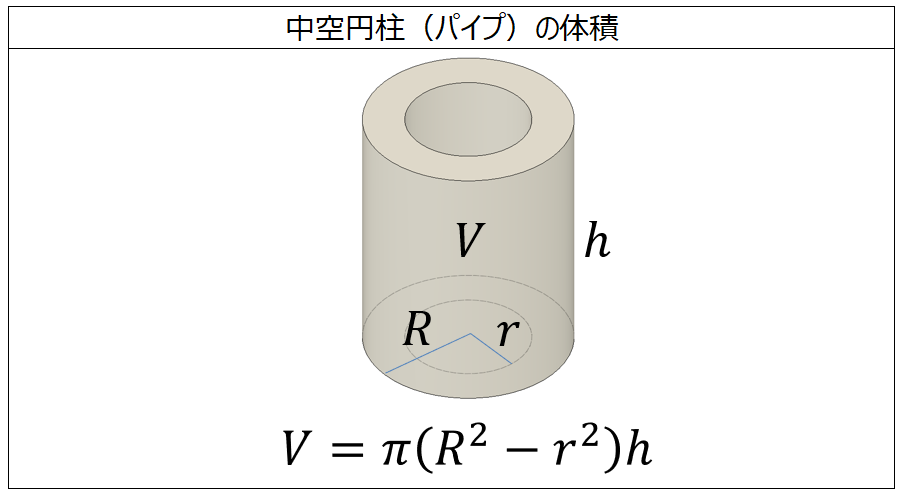



体積の計算 中空円柱 パイプ 製品設計知識




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



1




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 数学ノート




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ



円筒の体積計算 デジタル教科書 電子教科書




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角柱や円柱の表面積の求め方を教えてください Clear




丸棒の重量 円柱の体積と重量の求め方 鉄の場合




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



円柱の体積 簡単に計算できる電卓サイト




濃度 の計算が苦手な方へ 元研究員がわかりやすく解説 ページ 3 4 Study Z ドラゴン桜と学ぶwebマガジン




体積の求め方 計算公式一覧




円柱の体積の求め方 公式と計算例



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




円柱の展開図 Youtube



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




円柱の体積の求め方 公式 小学生 中学生の勉強




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室




角錐 円錐の体積と表面積の公式 数学fun



3



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




円柱の体積の求め方 公式 小学生 中学生の勉強




円柱の内容積の求め方 あるテストの問題で 円柱の内容積を求めよとあ 数学 教えて Goo




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




2 を途中式を含めて教えてください Clear




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



質量と比重




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
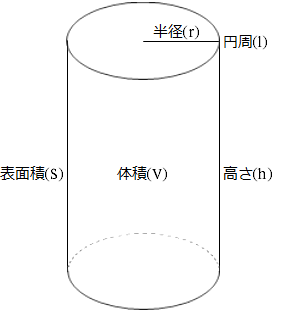



Excel関数 直円柱の体積や表面積を計算するrccylinderカスタムワークシート関数群 黒い箱の中




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




公式を図解 すい体の体積 円すいの表面積の求め方




円柱の体積の求め方 公式 小学生 中学生の勉強




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
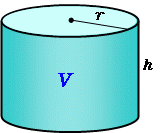



直円柱の体積 高精度計算サイト
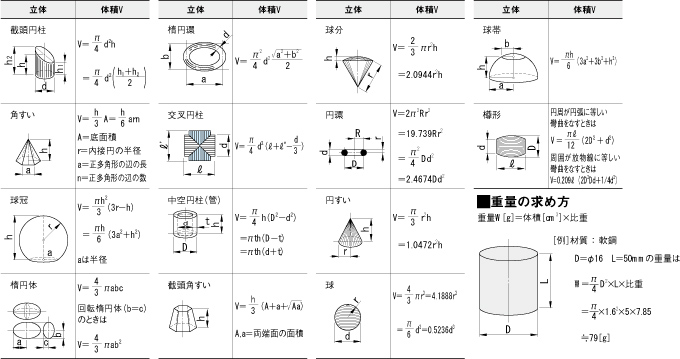



体積 重量の求め方 技術計算サイトの案内 Jis Z 02 より抜粋 ミスミ メカニカル加工部品
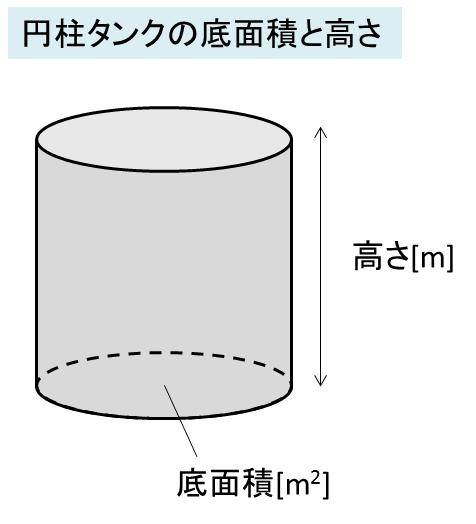



燃料タンクなどの円筒型タンクや角タンクの容量の計算方法




体積の求め方 計算公式一覧



0 件のコメント:
コメントを投稿