Ans (xy1) (xy1) By using a 2 − b 2 = ( a − b) ( a b) The only thing which is different from this is you must have to arrange it into this form So below are the steps x 2 − ( y 2 2 y 1) ==>we take common x 2 − ( y 1) 2 ==> ( a 2 2 a b b 2) = ( a b) 2
Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2-Here is another solution Case 2 x,y= 1 y (x1) => x^y y 1 >= xy wonderful, in case the exponent is between 0 and 1, the Bernoulli inequality is reversed, ie (1x)^r views around the world You can reuse this answer Creative Commons License
Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | 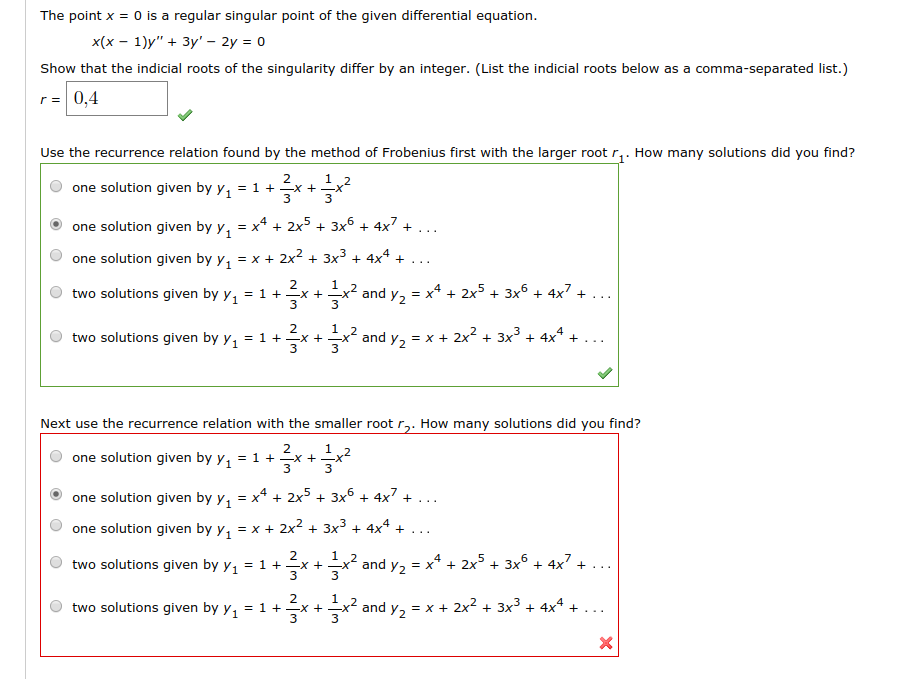 |  |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  | |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 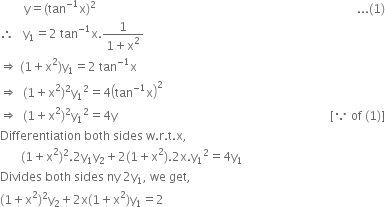 |  |
「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
Answer You cannot for all possible values of x > 2 and y > 2 prove this I only have to find one instance where this is not true (a counterexample) to disprove this if x = 3 and y = 6 5x 3y = 15 18 = 3 3 is not greater than 1 This disproves what you are stating I'm trying to prove that x n y n is divisible by (xy), when x and y are integers, and n is a positive, odd integer I previously proved that x ny n was divisible by (xy) with induction, so I figured a similar method would make sense here, but I end up going in circles this is what I tried Since n is an positive integer x n y n can be rewritten as x 2a1 y 2a1, where a is a positive





0 件のコメント:
コメントを投稿